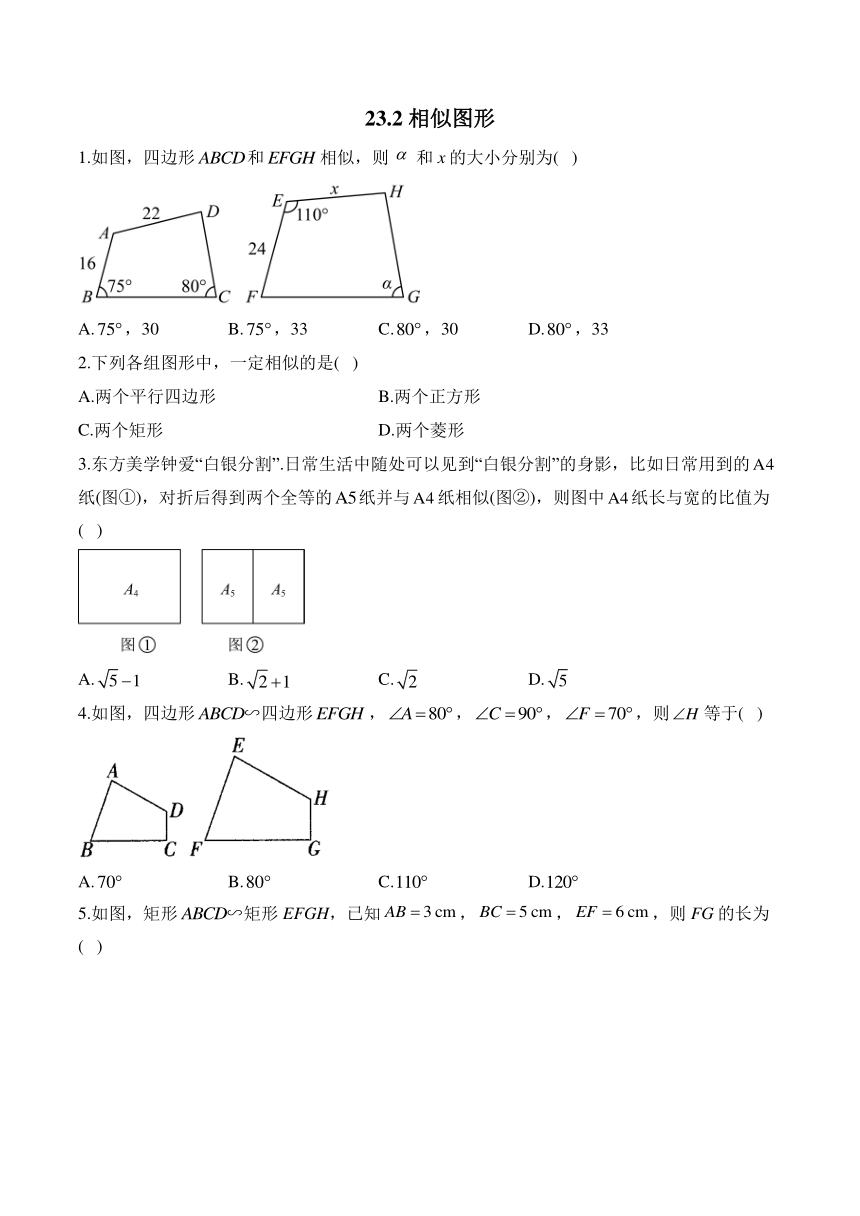
23.2 相似图形 1.如图,四边形和相似,则和x的大小分别为( ) A.,30 B.,33 C.,30 D.,33 2.下列各组图形中,一定相似的是( ) A.两个平行四边形 B.两个正方形 C.两个矩形 D.两个菱形 3.东方美学钟爱“白银分割”.日常生活中随处可以见到“白银分割”的身影,比如日常用到的纸(图①),对折后得到两个全等的纸并与纸相似(图②),则图中纸长与宽的比值为( ) A. B. C. D. 4.如图,四边形四边形,,,,则等于( ) A. B. C. D. 5.如图,矩形矩形EFGH,已知,,,则FG的长为( ) A. B. C. D. 6.已知四边形四边形,四边形与四边形的周长分别为24、36,则它们对角线AC与的比为( ) A.2:3 B.3:2 C.4:9 D.9:4 7.两个相似多边形的面积比是,若较小多边形的周长为,则较大多边形的周长为( ) A. B. C. D. 8.如图,在矩形中,,,E,F分别是,上的点,且,两动点M,N都以的速度分别从点C,F出发沿,向点B,E运动.当矩形与矩形相似时,点M,N运动的时间为( ) A.或 B.或 C.或 D.或或 9.如果两个相似多边形面积之比为,则它们的边长之比为_____. 10.如图,取一张长为a,宽为b的矩形纸片,将它对折两次后得到一张小矩形纸片.若要使小矩形与原矩形相似,则原矩形纸片的边a、b应满足的条件是_____. 11.一个六边形六边长分别为3,4,5,6,7,8,另一个与它相似的六边形的最短边为6,则其周长为_____. 12.如图,在正方形网格上有两个相似三角形和,则的度数为_____. 13.如果把两条直角边分别为,的直角三角形按相似比进行缩小,得到的直角三角形的两条直角边的长和面积各是多少? 14.如图,四边形EFGH相似于四边形KLMN,求,,的度数以及x,y,z的值. 答案以及解析 1.答案:D 解析:由图可知,,,,,,, 四边形和相似, ,, 即, , 故答案为:D. 2.答案:B 解析:A、任意两个平行四边形对应边的比不一定相等,对应角也不一定相等,故不一定相似,此选项不符合题意; B、任意两个正方形的对应角相等,对应边的比也相等,故一定相似,故此选项符合题意; C、任意两个矩形对应角相等,但对应边的比不一定相等,故不一定相似,此选项不符合题意; D、任意两个菱形的对应边的比相等,但对应角不一定相等,故不一定相似,此选项不符合题意; 故选:B. 3.答案:C 解析:设纸长与宽分别为x,y, 则纸长与宽分别为y,, ∵对折后得到两个全等的纸并与纸相似, ∴, 即:, ∴, ∴, 故选:C. 4.答案:D 解析:四边形四边形EFGH,,,,,, ,故选D. 5.答案:B 解析:矩形矩形EFGH,,,.故选B. 6.答案:A 解析:如图,连接AC、 ′ 四边形ABCD与四边形相似, =,, , ===, 故选:A. 7.答案:C 解析:两相似多边形的面积比是, 两相似多边形的相似比为:, 两相似多边形的周长比为:, 较小多边形的周长为, 较大多边形的周长为:. 故选:C. 8.答案:B 解析:∵,, ∴, 设矩形与矩形相似时,运动时间为, 当矩形矩形时,, ∴ 解得, 当矩形矩形时, ∴, 解得:. 故选:. 9.答案: 解析:∵相似多边形的面积比等于相似比的平方,面积比为, ∴对应边的比为, 故答案是:. 10.答案: 解析:对折两次后的小长方形的长为b,宽为, ∵小矩形与原矩形相似, ∴, ∴, 故答案为:. 11.答案:66 解析:一个六边形六边长分别为3,4,5,6,7,8,另一个与它相似的六边形的最短边为6, 两个相似多边形的相似比, , 解得. 故答案为:66. 12.答案:135° 解析:, , 又, . 故答案是:135°. 13.答案:缩小后的直角三角形的两条直角边的长分别为和,面积为 解析:设缩小后的直角三角形的两条直角边分别为和,面积为, 由题意,得,. 解得,,. 缩小后的直角三角形的两条直角边的长分别为和,面积为. 14.答案:,,,,, 解析:四边形EFGH相似于四边形KLM ... ...
~~ 您好,已阅读到文档的结尾了 ~~