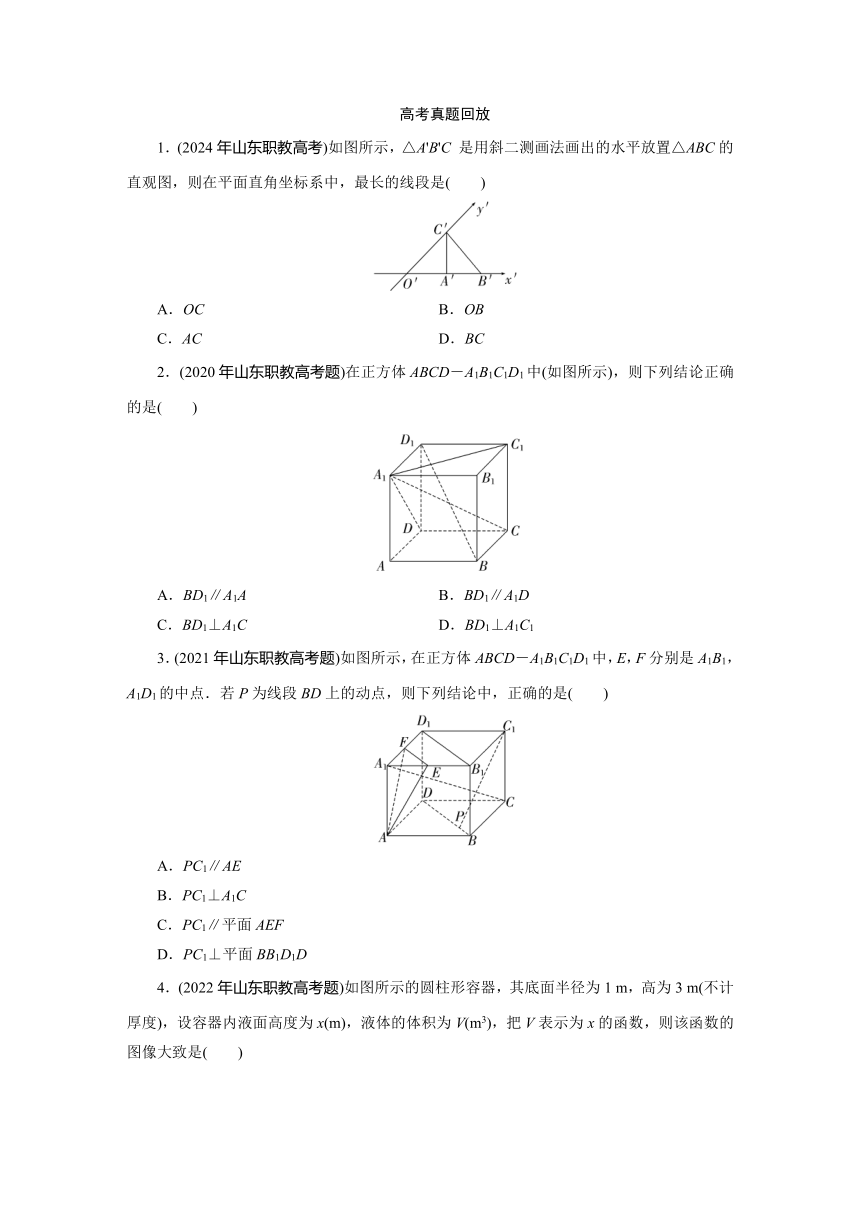
高考真题回放 1.(2024年山东职教高考)如图所示,△A'B'C 是用斜二测画法画出的水平放置△ABC的直观图,则在平面直角坐标系中,最长的线段是( ) A.OC B.OB C.AC D.BC 2.(2020年山东职教高考题)在正方体ABCD-A1B1C1D1中(如图所示),则下列结论正确的是( ) A.BD1∥A1A B.BD1∥A1D C.BD1⊥A1C D.BD1⊥A1C1 3.(2021年山东职教高考题)如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,A1D1的中点.若P为线段BD上的动点,则下列结论中,正确的是( ) A.PC1∥AE B.PC1⊥A1C C.PC1∥平面AEF D.PC1⊥平面BB1D1D 4.(2022年山东职教高考题)如图所示的圆柱形容器,其底面半径为1 m,高为3 m(不计厚度),设容器内液面高度为x(m),液体的体积为V(m3),把V表示为x的函数,则该函数的图像大致是( ) 5.(2024年山东职教高考)如图所示正三棱锥S-ABC的棱长都是2,D是SC的中点,结出下列个结论: ①SA∥BD ②AB⊥SC ③SC与平面ABC所成的角是60° ④正三棱锥S-ABC的体积是其中结论正确的序号是( ) A.①② B.①③ C.③④ D.②④ 6.(2020年山东职教高考)已知球的直径为2,则该球的体积是_____. 7.(2021年山东职教高考)已知正四棱锥的底面边长为1,侧棱长为2,则该正四棱锥的表面积等于_____. 8.(2022年山东职教高考)若底面边长为4的正四棱锥与棱长为2的正方体体积相等,则正四棱锥的高等于_____. 9.(2024年山东职教高考)如图,已知长方体ABCD-A1B1C1D1的底面是正方形,AB=3侧棱AA1=4,E,F分别是AD1,CD1的中点. (1)证明EF⊥BD. (2)求异面直线AD1与BC所成角的大小(精确到1°). 10.(2020年山东职教高考题)已知点E,F分别是正方形ABCD的边AB、BC的中点,把EFCD沿EF折起,使二面角C-EF-B为直二面角,如图所示. (1)若点G,H分别是AC,BF的中点,求证:GH∥平面EFCD; (2)求直线AC与平面ABFE所成角的正弦值. 11.(2021年山东职教高考题)在四棱锥S-ABCD中,已知底面ABCD是正方形,SA⊥面ABCD,∠SDA=60°,如图所示. (1)求证:AB⊥SD; (2)若E,F分别是AB,SC的中点,求直线EF与AD所成角的大小. 12.(2022年山东职教高考题)如图所示,在正方体ABCD-A1B1C1D1中,P是棱B1B上的点,求证: (1)AC∥平面A1PC1; (2)AC⊥D1P. 13.(2023年山东职教高考题)如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,且D,E,F分别是SC,AC,BC的中点,△SAB的边长都是2,SC=4. (1)求证:平面DEF∥平面SAB; (2)求直线SC与平面ABC所成角的正弦值. 答案 1.D 解析 根据斜二测画法△ABC原图为直角三角形且BC为斜边,故选C. 2.D 3.B 解析 易证A1C⊥BC1,A1C⊥BD,所以A1C⊥平面C1BD,又因为C1P 平面C1BD,所以A1C⊥C1P. 4.A 解析 根据圆柱的体积公式得:V=sh=πr2x=πx为一次函数,图像为一条直线,当x=3时体积最大,所以选A. 5.D 解析 对于①:SA和BD互为异面直线,所以①错误对于②:取底面ABC中心O,连接SO,CO,则有SO⊥底面ABC,所以SO⊥AB,又因为CO⊥AB,且,所以有AB⊥面SOC,所以AB⊥SC,所以②正确.对于③:由②知SO⊥底面ABC,所以∠SCO即为SC与平面ABC所成的角,边长为2,所以,CO=××2=,SO===,所以sin∠SCO==,明显不是60°,③错误.对于④:由③知SO=,所以正三棱锥S-ABC的体积为:V=sh=××2××=,故④正确.所以选D. 6.π 解析 因为直径为2,所以半径为1,由球的体积公式得:V=πR3=π. 7.+1 解析 由题意知:正四棱锥的斜高为=,所以S侧=4××1×=,又因为S底=1,所以正四棱锥的表面积=S侧+S底=+1. 8. 解析 由锥体体积公式得:V=Sh=×16×h=8,解得h=. 9.(1)证明:连接AC,BD交于O,因为长方体的底面为正方形,所以AC⊥BD,又因为E,F ... ...
~~ 您好,已阅读到文档的结尾了 ~~