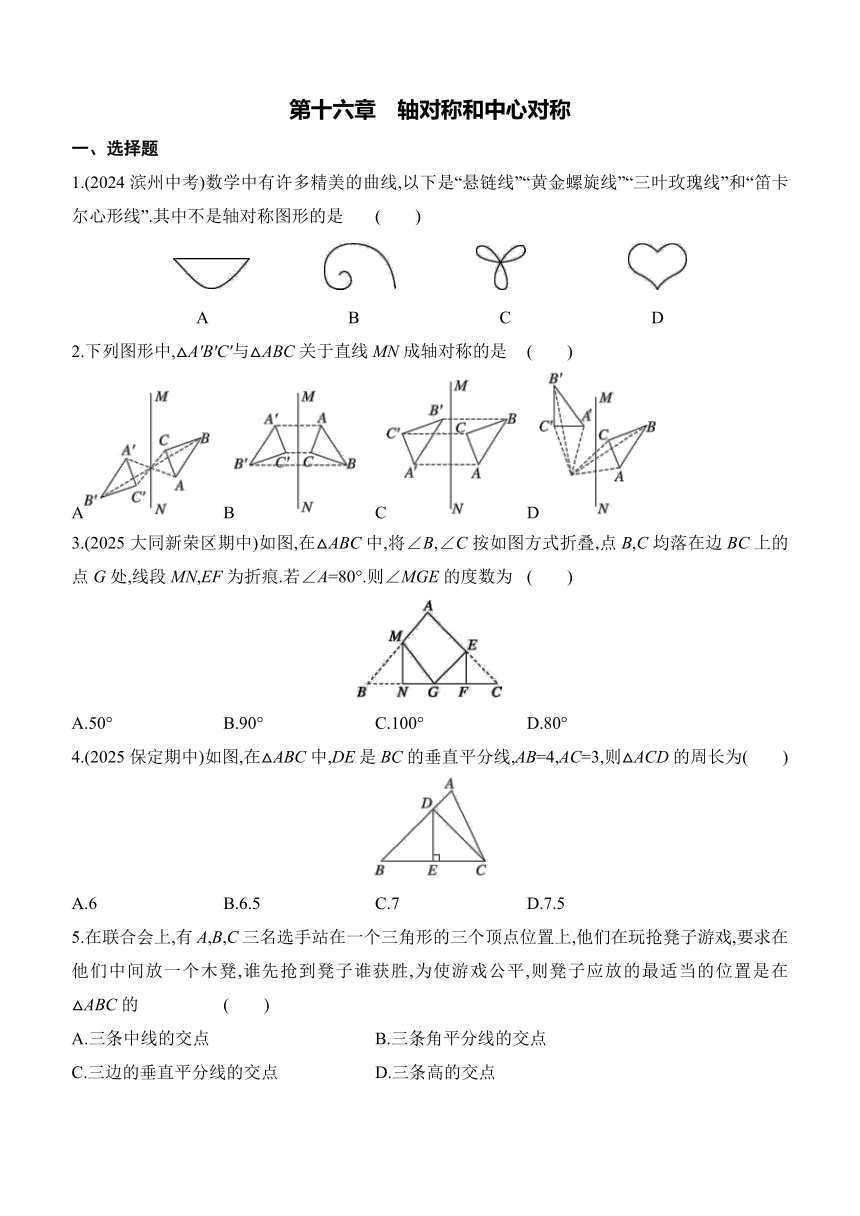
第十六章 轴对称和中心对称 一、选择题 1.(2024滨州中考)数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是 ( ) A B C D 2.下列图形中,△A'B'C'与△ABC关于直线MN成轴对称的是 ( ) A B C D 3.(2025大同新荣区期中)如图,在△ABC中,将∠B,∠C按如图方式折叠,点B,C均落在边BC上的点G处,线段MN,EF为折痕.若∠A=80°.则∠MGE的度数为 ( ) A.50° B.90° C.100° D.80° 4.(2025保定期中)如图,在△ABC中,DE是BC的垂直平分线,AB=4,AC=3,则△ACD的周长为( ) A.6 B.6.5 C.7 D.7.5 5.在联合会上,有A,B,C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的 ( ) A.三条中线的交点 B.三条角平分线的交点 C.三边的垂直平分线的交点 D.三条高的交点 6.如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点,再分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是 ( ) A.CA=CB B.CD⊥直线l C.点C,D关于直线l对称 D.点A,B关于直线CD对称 7.(2025沧州期末)如图,BO,CO分别平分∠ABC,∠ACB,OD⊥BC于点D,OD=2,△ABC的周长为28,则△ABC的面积为 ( ) A.28 B.14 C.21 D.7 二、填空题 8.(2025张家口万全区期中)如图,有一个英语单词,四个字母都关于直线l对称,请写出这个单词: . 9.如图,在直角三角形ABC中,∠C=90°,以顶点A为圆心,以适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,适当长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=3,AB=8,则△ABD的面积是 . 10.如图,在△ABC中,AB的垂直平分线交AC于点D,若△BCD的周长为5,BC=2,则AC的长为 ,边AB长的取值范围是 . 三、解答题 11.下列各图中的单位小正方形的边长都等于1,并且都已经填充了一部分阴影,请按要求对以下图形进行填充. (1)使得图1成为轴对称图形. (2)使得图2成为至少有4条对称轴且阴影部分面积等于3的图形. (3)使得图3成为至少有2条对称轴且面积不超过6的图形. 图1 图2 图3 12.如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE. (1)若∠BAE=40°,求∠C的度数. (2)若△ABC的周长为13 cm,AC=6 cm,求DC的长. 13.如图1,O为直线AB上一点,过点O作射线OC,使∠BOC=50°.现将一个直角三角板的直角顶点放在点O处,一边OD与射线OB重合,如图2. (1)∠EOC= . (2)如图3,将三角板DOE绕点O逆时针旋转一定角度,当OC是∠BOE的平分线时,求∠BOD的度数. (3)将三角板DOE绕点O逆时针旋转,设旋转角度为α(0°<α<90°), ①∠AOE= ,∠COD= ;(用含α的代数式表示) ②是否有某个时刻满足∠COD=∠AOE 如果有,求∠BOD的度数;如果没有,请说明理由. 【详解答案】 1.B 2.B 解析:根据轴对称的性质,结合四个选项,只有B选项中对应点的连线被对称轴MN垂直平分,所以B是符合要求的.故选B. 3.D 解析:∵线段MN,EF为折痕,∴∠B=∠MGB,∠C=∠EGC, ∵∠A=80°,∴∠B+∠C=180°-80°=100°,∴∠MGB+∠EGC=∠B+∠C=100°,∴∠MGE=180°-100°=80°.故选D. 4.C 解析:∵DE是BC的垂直平分线,∴DB=DC.∴△ACD的周长=AD+DC+AC=AD+DB+AC=AB+AC=4+3=7.故选C. 5.C 解析:∵三角形的三条垂直平分线的交点到三角形各顶点的距离相等,∴凳子放在△ABC的三边的垂直平分线的交点处最适当.故选C. 6.C 解析:由作法得CD垂直平分AB,所以B选项正确;因为CD垂直平分AB,所以CA=CB,所以A,D选项正确;因为AD不一定等于AC,所以C选项错误.故选C. 7.A 解析:如图,连接OA,作OE⊥AB于点E,作OF⊥AC于点F.∵BO,CO分别平分 ... ...
~~ 您好,已阅读到文档的结尾了 ~~