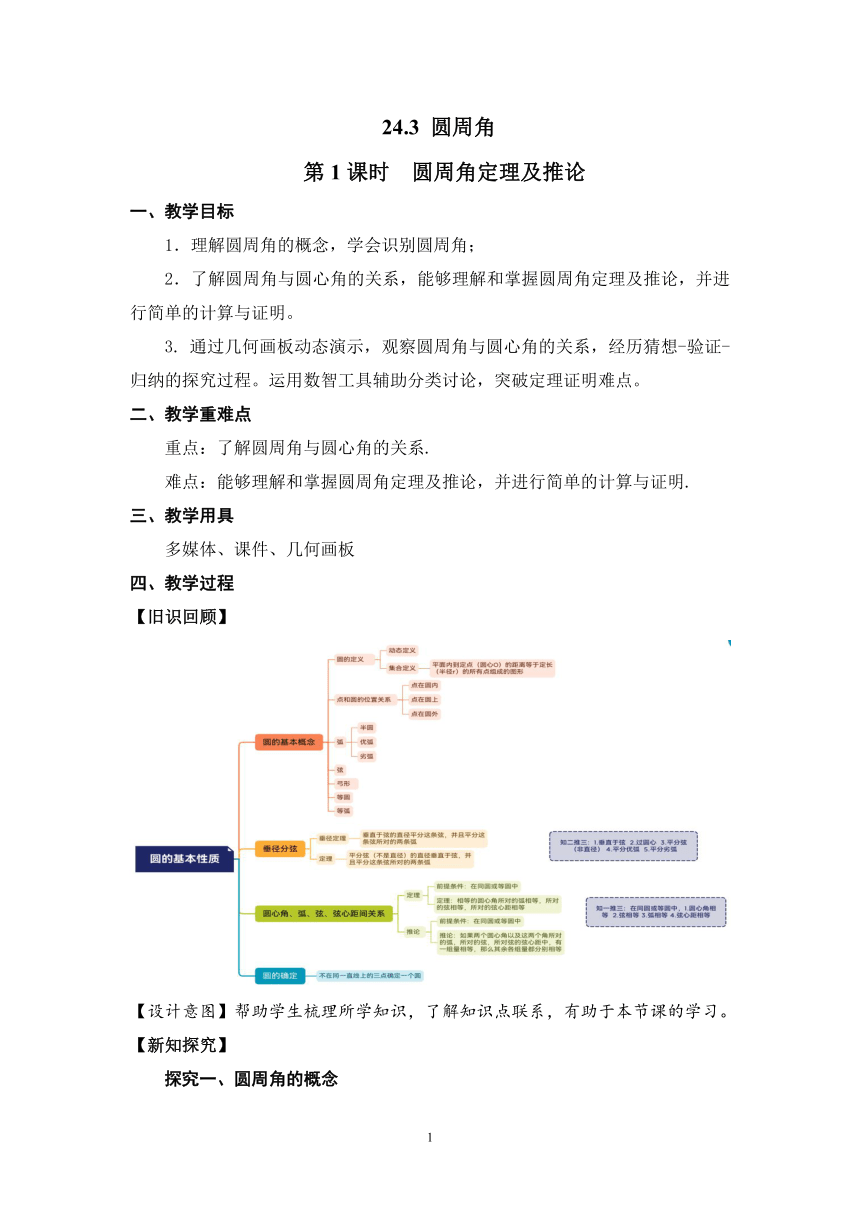
24.3 圆周角 第1课时 圆周角定理及推论 一、教学目标 1.理解圆周角的概念,学会识别圆周角; 2.了解圆周角与圆心角的关系,能够理解和掌握圆周角定理及推论,并进行简单的计算与证明。 3. 通过几何画板动态演示,观察圆周角与圆心角的关系,经历猜想-验证-归纳的探究过程。运用数智工具辅助分类讨论,突破定理证明难点。 二、教学重难点 重点:了解圆周角与圆心角的关系. 难点:能够理解和掌握圆周角定理及推论,并进行简单的计算与证明. 三、教学用具 多媒体、课件、几何画板 四、教学过程 【旧识回顾】 【设计意图】帮助学生梳理所学知识,了解知识点联系,有助于本节课的学习。 【新知探究】 探究一、圆周角的概念 思考:将圆心角顶点向上移,直至与⊙O相交于点C 观察得到的∠ACB有什么特征? 师生活动:教师提出问题,学生回答。对于第1题学生回答“顶点在圆心的角叫做圆心角。”教师强调“顶点在圆上,且两边都和圆各另有一个交点”。第2题圆心角的度数和它所对的弧的度数相等,教师可简单说明一下为什么。 【设计意图】通过对于圆心角的两个问题的回顾,为下面学习圆周角的概念提供了方法,学生可类比理解圆周角的特征:顶点在圆心上,两边与圆各有一个交点。 师生活动:让学生观察以上几种情况,辨析哪些是圆周角,进一步强调圆周角的两个特征:①顶点在圆上;② 两边都与圆还另有一个交点. 教师板书圆周角定义:顶点在圆上,并且两边都与圆还各有一个交点的角叫做圆周角。 【设计意图】通过观察,类比,讲解,使学生基本了解圆周角定义及其两个特征。紧接着提出问题,巩固概念,对于学生的回答,教师要用鼓励性的语句进行评价,激发学生学习数学的兴趣,增强学生学习数学的信心,真正掌握圆周角的概念。 探究二、圆周角和圆心角的关系 数智技术融合设计 1. 第一课时:圆周角定理发现 活动1:动态观察与猜想 使用几何画板动态演示:拖动圆周角顶点,观察角与对应弧的关系。 问题链: 当圆心在圆周角内部/外部/边上时,圆周角与圆心角有何数量关系? 同弧所对的圆周角是否相等? 技术工具:几何画板、动态测量工具(实时显示角度数值)。 活动2:数据采集与验证 学生分组操作几何画板,记录不同位置圆周角与圆心角的度数,填写电子实验报告(如Google Forms)。 技术工具:数据可视化工具(生成角度关系图表)。 2. 第二课时:定理证明与分类讨论 活动1:辅助线智能提示 通过几何画板提供辅助线添加提示,引导学生完成三种位置关系的证明。 技术工具:分步动画演示、错误提示系统。 活动2:虚拟实验与协作学习 使用Mentimeter实时收集学生证明思路,运用Xmind生成思维导图,全班协作优化证明过程。 技术工具:Mentimeter、Xmind。 过程:如图,△ABC是等边三角形, ⊙O是其外接圆。你能发现∠BAC和∠BOC的大小有什么关系吗? 师生活动:教师投影,学生思考,得出结论: ∠A=∠BOC或∠BOC=2∠A. 即所对的圆周角等于它所对圆心角的一半. 学生结论的获得可能是通过度量也可能是推理,教师均给予鼓励. 教师画图并板书推理过程: 在图中 ∵OA=OC,∴∠A=∠OCA. 又∠BOC=∠A+∠OCA=2∠A, ∴∠A=∠BOC. 教师提问:我们能否据此就说“一条弧所对的圆周角等于它所对圆心角的一半” 学生回答:不行,因为不能用特殊来代替一般。 教师提问:刚才我们看到的是圆心在圆周角一边时情形,那么圆心与圆周角的位置有哪些情形呢? 教师演示几何画板,让学生自主归纳得出:共有三种情形,即圆心在圆周角的一条边上,圆心在圆周角的内部和圆心在圆周角的外部。 教师投影出示圆心与圆周角的三种位置关系,并提问:另外两种情形中也有“所对的圆周角等于它所对圆心角的一半”吗?学生思考,教师在黑板上画 出图形。 教师引导学生把圆心在圆周角 ... ...
~~ 您好,已阅读到文档的结尾了 ~~