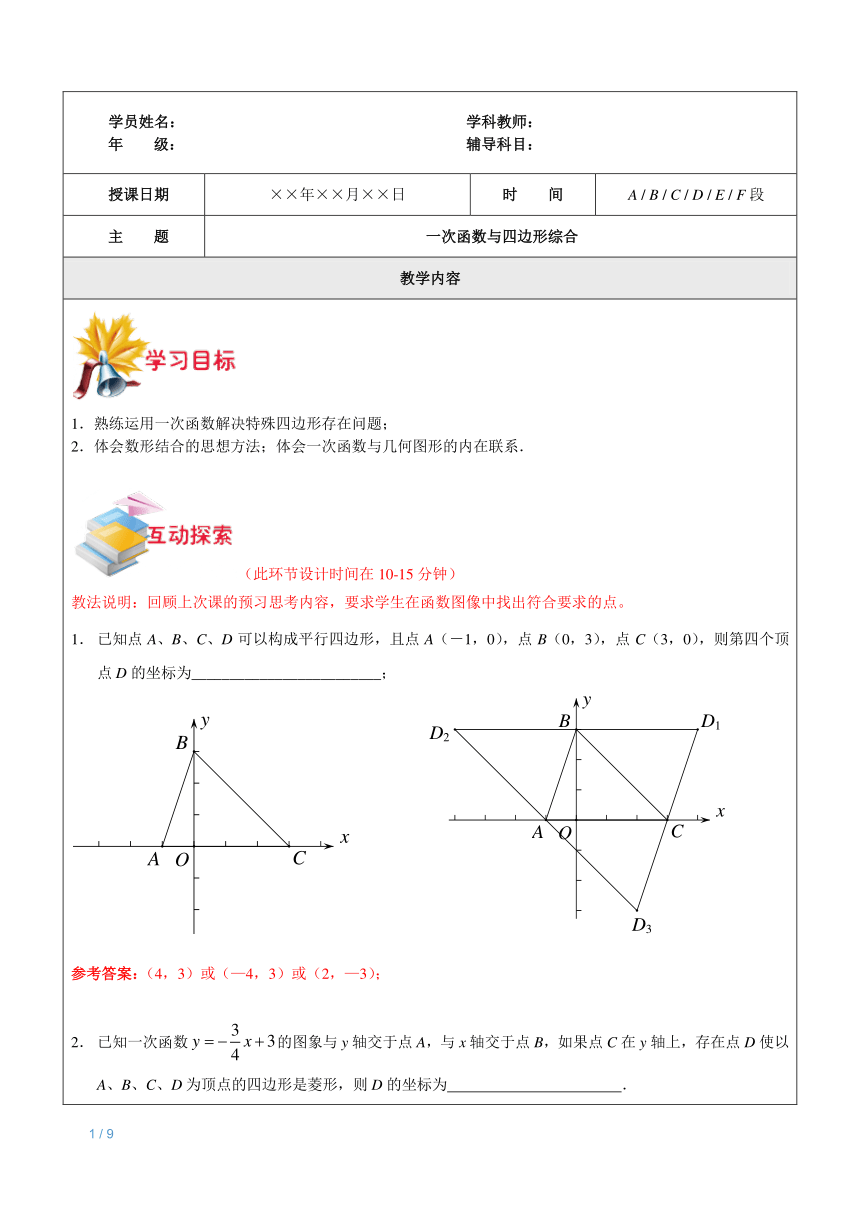
学员姓名: 学科教师: 年 级: 辅导科目: 授课日期 ××年××月××日 时 间 A / B / C / D / E / F段 主 题 一次函数与四边形综合 教学内容 1.熟练运用一次函数解决特殊四边形存在问题; 2.体会数形结合的思想方法;体会一次函数与几何图形的内在联系. (此环节设计时间在10-15分钟) 教法说明:回顾上次课的预习思考内容,要求学生在函数图像中找出符合要求的点。 已知点A、B、C、D可以构成平行四边形,且点A(-1,0),点B(0,3),点C(3,0),则第四个顶点D的坐标为_____; 参考答案:(4,3)或(—4,3)或(2,—3); 已知一次函数的图象与y轴交于点A,与x轴交于点B,如果点C在y轴上,存在点D使以A、B、C、D为顶点的四边形是菱形,则D的坐标为 . 参考答案:; (此环节设计时间在50-60分钟) ( E A O x y B C D )例题1:如图,在平面直角坐标系中,四边形ABCD为菱形,点A的坐标为(0,1),点D在轴上,经过点B的直线与AC相交于横坐标为2的点E. (1)求直线AC的表达式; (2)求点B、C、D的坐标. 参考答案:(1)∵点直线经过横坐标为2的点E,∴E(2,2). 由点A(0,1),设直线AC的表达式为, ∴;∴直线AC的表达式为. (2)设点C的坐标为(), ∵在菱形ABCD中,BC//AD,∴点B的坐标为(). ∵BA=BC,∴; ∴. ∴. ∴点B、C的坐标分别为()、(). ∵AD=BC=15,∴OD=16,∴D(0,16). 例题2:已知:直线与x轴交于点A,与y轴交于点B。点C的坐标为(0,—2),线段AB上有一动点P,过点C、P作直线l。 (1)如图,当PB=PC时,求点P的坐标; (2)在(1)的条件下,平面直角坐标系内是否存在这样的点Q,使以P、B、C、Q四个点为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由。 参考答案: (1)作PH⊥y轴,∵PB=PC ∴H为BC中点; ∴H(0,2) ∴点P的坐标 (2),, 例题3:已知一次函数的图像与x轴、y轴分别相交于点A、B.梯形AOBC的边AC = 5. (1)求点C的坐标; (2)如果点A、C在一次函数(k、b为常数,且k<0)的图像上,求这个一次函数的解析式. 参考答案: (1)A(8,0),B(0,4). 在梯形AOBC中,OA=8,OC=4,AC=5. 当AC//OB时,点C的坐标为(8,5). 当BC//OA时,设点C(x,4). ∴ 这时点C的坐标为(5,4)或(11,4). ∴点C的坐标为(8,5)或(5,4)或(11,4). (2)∵点A、C在一次函数(k<0)的图象上, ∴点(8,5)与(11,4)都不符合题意,只有当C为(5,4)时,k<0. ∴ ∴ ∴这个一次函数的解析式为. ※例题4:在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=OC=6,分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系,D、F分别为线段OC,x轴上的点,OD=5,OF=10,直线DF交OB于点E. (1)求直线DE的解析式并求出E点坐标; (2)点M是(1)中直线DE上的一个动点,在x轴上方的平面内是否存在另一个点N使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由. 参考答案:(1)直线DE的解析式为,点E的坐标为(2,4) (2)存在 ①如图1,当OD=DM=MN=NO=5时 设M点坐标为, ∴∴(正舍) ∴点M的坐标为 又∵MN∥x轴; ∴点N的坐标为 ②如图2,当OD=DN=NM=MO=5时, 延长NM交x轴于点P,则MP⊥x轴. ∵点M在直线上,∴设M点坐标为 在Rt△OPM中, ∴,解得(舍去), ∴点M的坐标为(4,3) ∴点N的坐标为(4,8) ③如图3,当OM=MD=DN=NO时,四边形OMDN为菱形. 联结NM交OD于点P则NM与OD互相垂直平分, ∴∴ ∴∴ ∴点N的坐标为 综上所述,x轴上方的点N有三个,分别为 此环节设计时间在30分钟左右(20分钟练习+10分钟互动讲解)。 1.如图,一次函数的图像与x、y轴分 ... ...
~~ 您好,已阅读到文档的结尾了 ~~