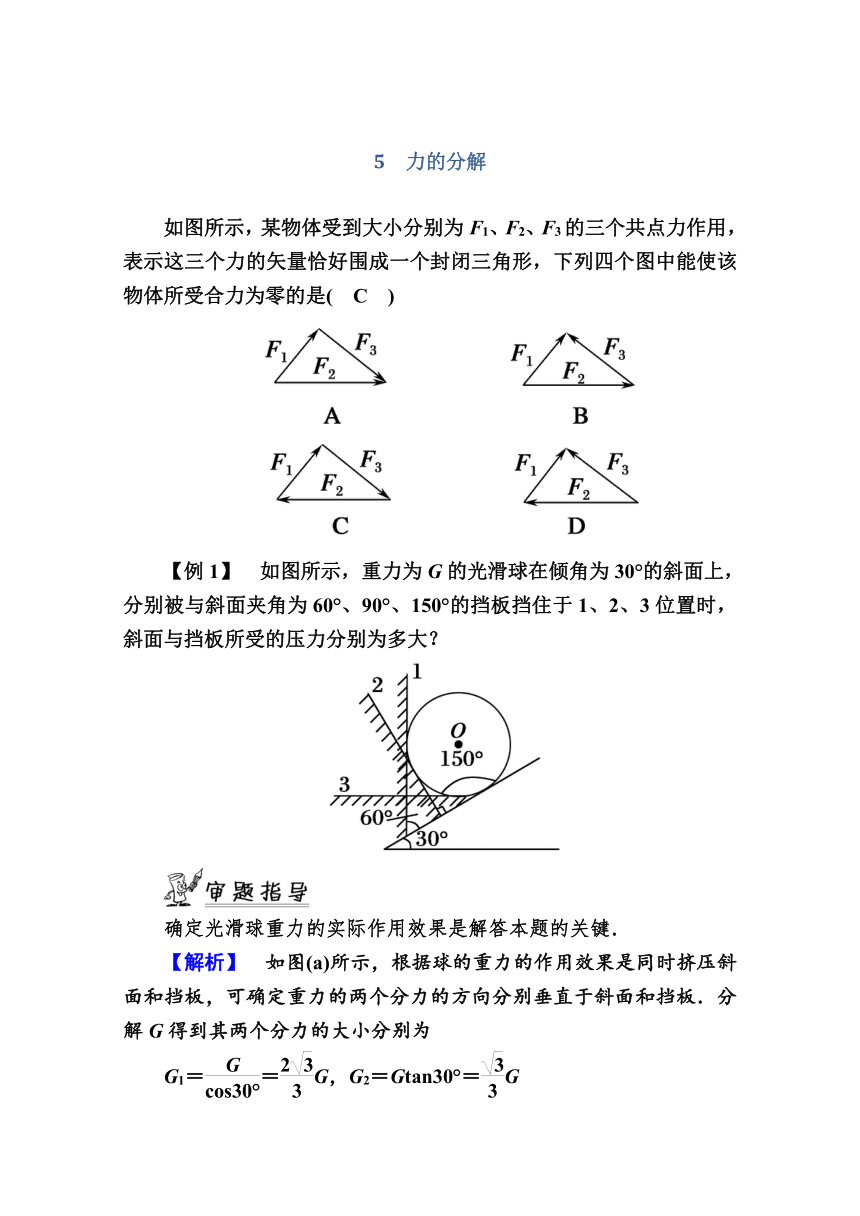
5 力的分解 如图所示,某物体受到大小分别为F1、F2、F3的三个共点力作用,表示这三个力的矢量恰好围成一个封闭三角形,下列四个图中能使该物体所受合力为零的是( C ) 【例1】 如图所示,重力为G的光滑球在倾角为30°的斜面上,分别被与斜面夹角为60°、90°、150°的挡板挡住于1、2、3位置时,斜面与挡板所受的压力分别为多大? 确定光滑球重力的实际作用效果是解答本题的关键. 【解析】 如图(a)所示,根据球的重力的作用效果是同时挤压斜面和挡板,可确定重力的两个分力的方向分别垂直于斜面和挡板.分解G得到其两个分力的大小分别为 G1==G,G2=Gtan30°=G 由此可知,斜面与挡板所受的压力大小分别为 N1=G,N2=G 如图(b)所示,同理得 N1′=G1′=Gcos30°=G,N2′=G2′=Gsin30°= 如图(c)所示,此时斜面不受压力,挡板所受的压力N2″的大小和方向与G相同,即N2″=G. 【答案】 见解析 总结提能 按力的实际作用效果分解力时,首先要确定力的作用效果,画出两个分力的方向,然后根据平行四边形定则作图,结合三角形的边角关系求解. 如图所示,用三根轻绳将质量为m的物体悬挂在空中,已知ac和bc与竖直方向的夹角分别为60°和30°,则绳ac和绳bc的拉力大小分别为多少? 解析:以m为研究对象,由二力平衡知竖直绳上的拉力大小为mg.则竖直绳拉c点的力F=mg,F作用于c点有两个作用效果,即拉紧绳ac和绳bc,故可将F沿ac和bc方向分解,求出绳ac和绳bc方向上的分力,也就求出了绳ac和绳bc的拉力. 将F进行分解如图所示,由三角形知识得 F1=Fsin60°=mg F2=Fsin30°=mg 由二力平衡得绳ac的拉力Fac=F2=mg 绳bc的拉力Fbc=F1=mg. 答案:mg mg 考点二 力的正交分解 1.概念 把力在两个互相垂直的方向上分解. 如图所示,将力F沿x轴和y轴两个方向分解,则Fx=Fcosα,Fy=Fsinα. 2.正交分解的目的 当物体受到多个力作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不方便.为此,我们建立一个直角坐标系,将各力在两条互相垂直的坐标轴上分解,分别求出两条坐标轴上的合力Fx和Fy,然后就可以由F=求合力了.所以,采用力的正交分解法的目的是通过先分解的方法求合力. 3.正交分解法求合力的步骤 (1)建立坐标系:以共点力的作用点为坐标原点建立直角坐标系,其中x轴和y轴的选择应使尽量多的力处在坐标轴上. (2)正交分解各力:将每一个不在坐标轴上的力分解到x轴和y轴上,并求出各分力的大小,如图所示. (3)分别求出x轴、y轴上各分力的合力,即Fx=F1x+F2x+F3x,Fy=F1y+F2y+F3y. (4)合力大小F=,设合力的方向与x轴的夹角为α,则tanα=. 4.正交分解法的优点 (1)借助数学中的直角坐标系对力进行描述. (2)几何图形是直角三角形,关系简单,计算简便. (3)分解多个力时,可将矢量运算化为代数运算. 【例2】 在同一平面内共点的四个力F1、F2、F3、F4的大小依次为19 N、40 N、30 N和15 N,方向如图所示,求它们的合力. ―→―→―→ 【解析】 如图(a)建立直角坐标系,把各个力分解在两个坐标轴上,并求出x轴和y轴上的合力Fx和Fy,有Fx=F1+F2cos37°-F3cos37°=27 N,Fy=F2sin37°+F3sin37°-F4=27 N, 因此,如图(b)所示,合力F=≈38.2 N,tanφ==1.即合力的大小约为38.2 N,方向与F1夹角为45°,斜向右上方. 【答案】 见解析 总结提能 正交分解中,坐标轴的选取方法: (1)研究水平面上的物体时,通常沿水平方向和竖直方向建立坐标轴. (2)研究斜面上的物体时,通常沿斜面方向和垂直斜面方向建立坐标轴. (3)研究物体在杆或绳的作用下转动时,通常沿杆(或绳)方向和垂直杆(或绳)的方向建立坐标轴. 如图所示,三个力作用于同一点O点,大小分别为F1=10 N,F2=20 N, ... ...
~~ 您好,已阅读到文档的结尾了 ~~