7.2 万有引力定律 教学设计

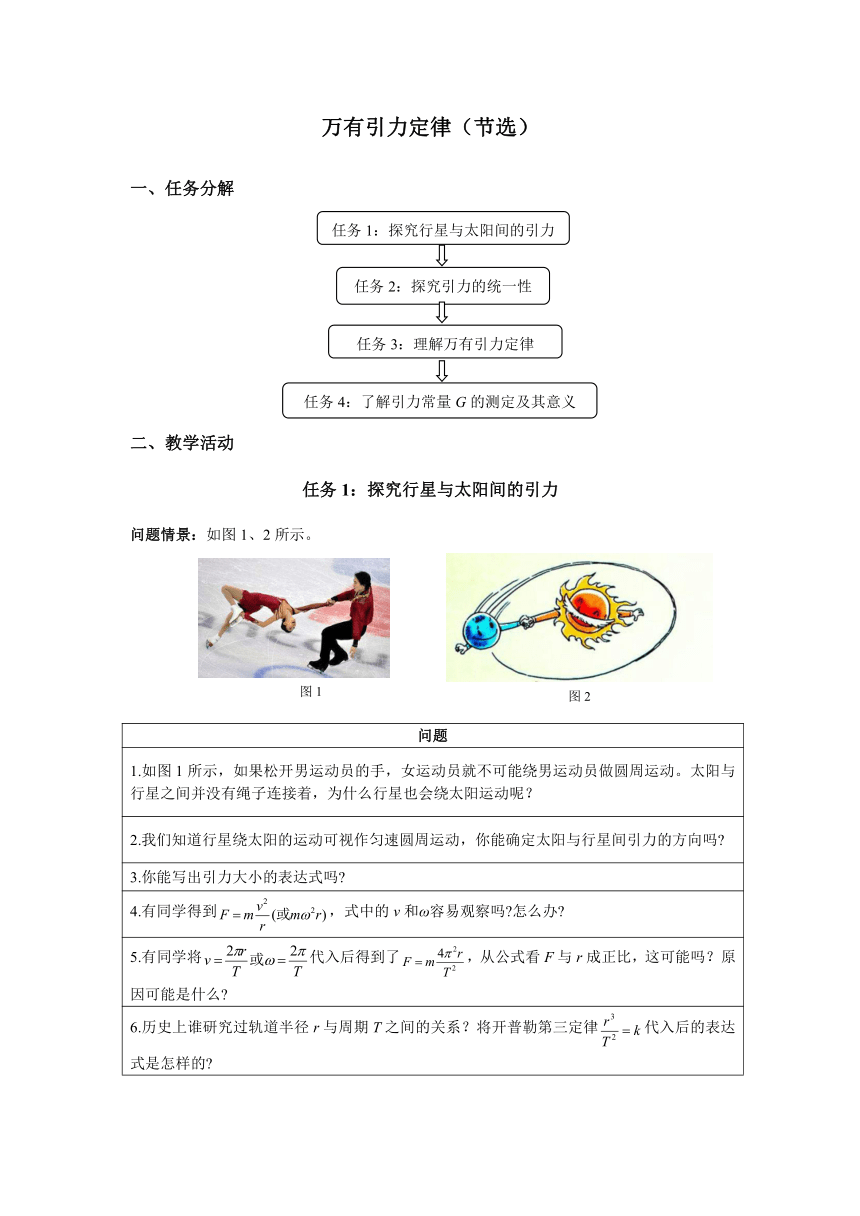
万有引力定律（节选） 一、任务分解 二、教学活动 任务1：探究行星与太阳间的引力 问题情景：如图1、2所示。 问题 1.如图1所示，如果松开男运动员的手，女运动员就不可能绕男运动员做圆周运动。太阳与行星之间并没有绳子连接着，为什么行星也会绕太阳运动呢？ 2.我们知道行星绕太阳的运动可视作匀速圆周运动，你能确定太阳与行星间引力的方向吗? 3.你能写出引力大小的表达式吗? 4.有同学得到，式中的v和ω容易观察吗?怎么办? 5.有同学将代入后得到了，从公式看F与r成正比，这可能吗？原因可能是什么? 6.历史上谁研究过轨道半径r与周期T之间的关系？将开普勒第三定律代入后的表达式是怎样的? 7.有同学得到，这个关系式令人困惑之处是：太阳对行星的吸引力为什么在表达式中只与m有关，而与太阳质量M无关? 8.有同学猜想与中心天体有关的k中可能包含太阳质量M。如何证明这一猜想呢?你还有什么路径（角度）可以尝试? 9.运动学公式（开普勒定律）和动力学公式（牛顿第二定律）我们都已经运用了，有同学想到了牛顿第三定律，从牛顿第三定律我们可以得到什么? 10.从牛顿第三定律我们可以得到F=F'，它能解决“为什么在表达式中只与m有关”这个问题吗？怎么办？ 11.有同学考虑到太阳与行星间的“相互作用地位相等，表达式应相似”得:，这是推理还是假设？ 12.根据牛顿第三定律，要始终满足F=F'，那么k及k'须满足什么条件? 13.有同学得到的条件为，你能写出太阳与行星间引力的表达式吗？ 14.历史上探究万有引力的科学家有哪些?他们的想法是什么?为什么他们不能像牛顿那样得到万有引力定律的表达式? 教学建议： （1）思维引导建议：根据圆周运动和牛顿运动定律可得到引力，因天文观测难以直接得到行星的运动速度v，但可以测得行星公转的周期T，据此将代入上式可得到，式中形式上F与半径r成正比，这显然不合理，说明周期T与半径r之间有一定的关系，故上式并不是最终的表达式。把开普勒第三定律变形为，代入上式得到，这个关系式令人困惑之处是：太阳对行星的吸引力为什么在表达式中只与m有关，而与太阳质量M无关？还有什么路径可以帮助我们深入探究？ 根据牛顿第三定律，有，但仍然无法解决F与太阳质量M无关这一问题。在已经没有推理之路可走的时候，什么可以帮助我们？只有假设：太阳与行星间的“相互作用地位相等，表达式应相似”得到：，根据牛顿第三定律，要始终满足F=F'，须，综合可得，太阳与行星间的引力，写成等式就是，式中G是比例系数，与太阳、行星都没有关系。历史上探究万有引力的科学家有不少，他们不能像牛顿那样得到万有引力定律的表达式主要是推导万有引力定律的研究基础是圆周运动知识和牛顿运动定律，对这些知识科学家们还缺乏，通过这一问题的讨论有助于学生认识到科学研究需要科学家集体的积累和某个科学家的创新突破。 （2）教学活动建议：对问题1、2、3、4，考虑到学生的已有知识，可采用独立思考并回答的方式。对问题5、6，可让学生先独立思考，再小组讨论后作答。对问题7、8、9、10、11、12、13，可先让学生独立思考后回答，其他同学补充，在必要的时候教师点拨引导。对问题14，可以教师先给出思考大致方向，然后小组讨论并交流。 任务2：探究引力的统一性 问题情景：播放苹果落地和月球绕地球运动小视频（或展示图片3、4）。 问题 1.为什么熟透的苹果会落地？ 2.为什么月亮能“悬挂”在高空？月亮是否受到地球的引力? 3.假设地球对月球的作用力与太阳对行星的作用力是同一种性质的力，其表达式应是怎样的? 4.月球在这个力的作用下做什么运动？其向心加速度的表达式应是怎样的？ 5.假设地球对树上苹果的吸引力也是同一种性质的力，其表达式是怎样的？ 6.苹果在这个力的作用下做什么运动？其加速度的表达式是怎样的 ... ...