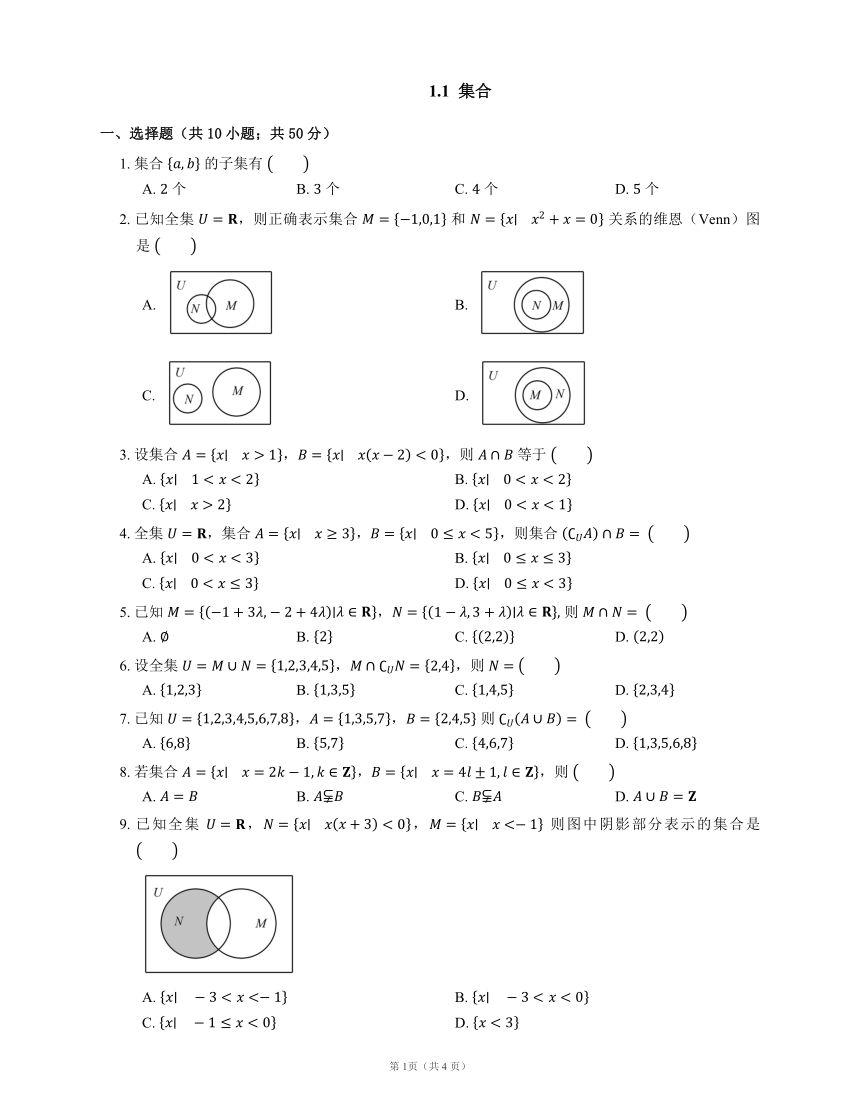
1.1 集合 一、选择题(共10小题;共50分) 1. 集合 的子集有 A. 个 B. 个 C. 个 D. 个 2. 已知全集 ,则正确表示集合 和 关系的维恩(Venn)图是 A. B. C. D. 3. 设集合 ,,则 等于 A. B. C. D. 4. 全集 ,集合 ,,则集合 A. B. C. D. 5. 已知 , 则 A. B. C. D. 6. 设全集 ,,则 A. B. C. D. 7. 已知 ,, 则 A. B. C. D. 8. 若集合 ,,则 A. B. C. D. 9. 已知全集 ,, 则图中阴影部分表示的集合是 A. B. C. D. 10. 有限集合 中元素的个数记作 .已知 ,,,,且 ,.若集合 满足 ,且 ,,则集合 的个数是 A. B. C. D. 二、填空题(共5小题;共25分) 11. 集合 共有 个子集. 12. 已知集合 ,,若 ,则实数 的取值范围为 . 13. 设 ,,,则 . 14. 已知集合 ,,且 ,则实数 的取值范围是 . 15. 设 , 是两个非空集合,定义 与 的差集为 ,则 . 三、解答题(共3小题;共39分) 16. 已知集合 ,集合 . (1); (2); (3). 17. 已知全集 ,,. (1)当 时,求 ,,. (2)若 ,求实数 的取值范围. 18. 数集 满足条件:若 ,则 . (1)若 ,试求 中必须含有的其它所有元素; (2)自己设计一个数属于 ,然后求出 中必须含有的其它所有元素; (3)从上面的解答过程中你能悟出什么道理,并大胆证明你发现的"道理". 答案 第一部分 1. C 2. B 3. A 4. D 【解析】,故 . 5. C 【解析】 6. B 【解析】由 可得集合 中不含有元素 ,,集合 中含有元素 ,,故 . 7. A 【解析】因为 ,, .所以 ,所以 . 8. A 9. C 【解析】,由图象知,图中阴影部分所表示的集合是 ,又 ,所以 ,所以 . 10. A 【解析】当 时,满足条件的 的个数为 个,当 时,满足条件的 的个数为 个,当 时,满足条件的 的个数为 个, 故满足条件的集合 的个数是 种. 第二部分 11. 【解析】集合 共有 个子集. 12. 【解析】,因为 ,所以 . 13. 【解析】因为 ,,, 所以 , 所以 . 14. 【解析】,由 可得 . 要注意这里的 可以取到边界值 . 15. 【解析】当 时,由于对任意的 ,都有 ,所以 ,所以 ;当 时, 表示在 中但不在 中的元素, 表示在 中但不在 中的元素,所以 . 第三部分 16. (1) . (2) . (3) . 17. (1) 当 时,, , 所以 ,, , 所以 . (2) 若 ,则 , 因为 , 所以 或 , 即 或 , 则实数 的取值范围为 . 18. (1) ,则 ,即 . 则 ,即 ;则 ,即 ; 所以 中必须含有的其它所有元素为 . (2) 答案不唯一,如:若 ,则 中必须含有的其它所有元素为 . (3) 分析以上结果可以得出, 中只要含有元素 ,就至少含有 个元素,分别是 ,且三个数的乘积为 . 证明如下: 若 ,则有 ,且 , 所以又有 ,且 ,进而有 . 又因为 (因为 ,则 ,而方程 无解), 同理 , 所以 中至少含有 个元素,它们分别是 ,且三个数的乘积是 . 第1页(共1 页) ... ...
~~ 您好,已阅读到文档的结尾了 ~~