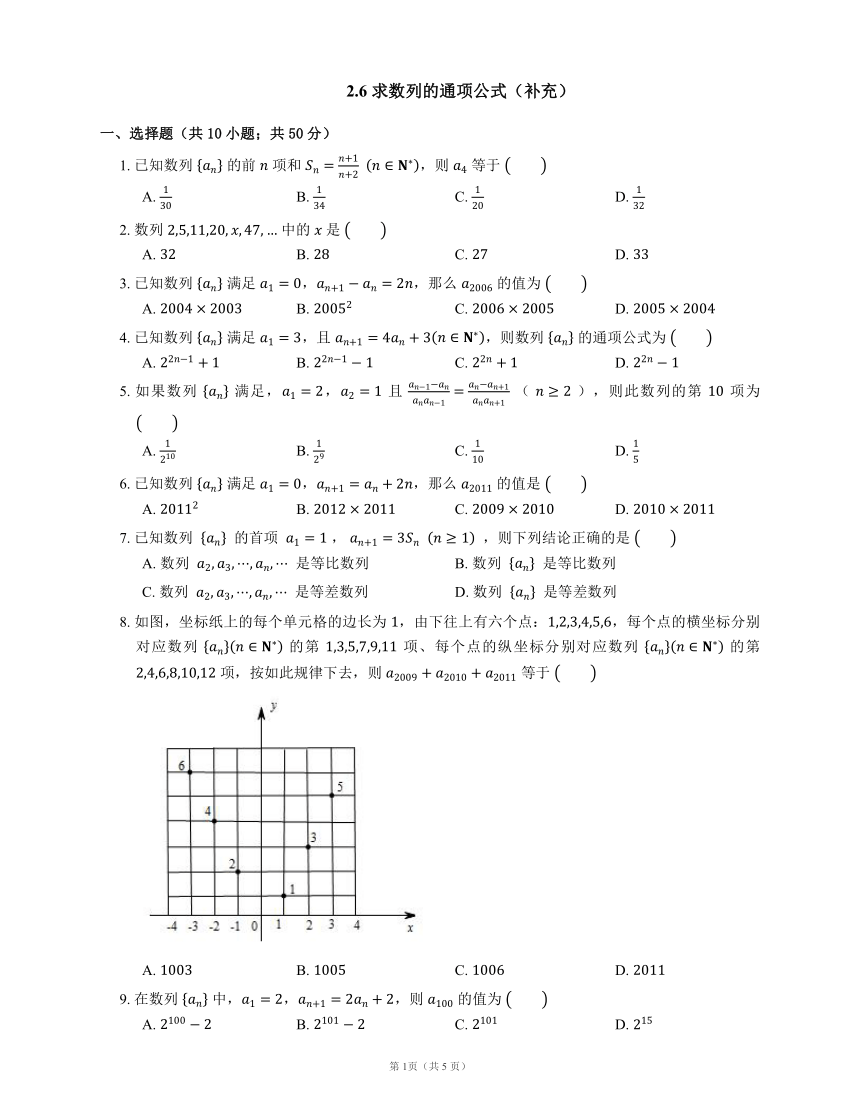
2.6 求数列的通项公式(补充) 一、选择题(共10小题;共50分) 1. 已知数列 的前 项和 ,则 等于 A. B. C. D. 2. 数列 中的 是 A. B. C. D. 3. 已知数列 满足 ,,那么 的值为 A. B. C. D. 4. 已知数列 满足 ,且 ,则数列 的通项公式为 A. B. C. D. 5. 如果数列 满足,, 且 ( ),则此数列的第 项为 A. B. C. D. 6. 已知数列 满足 ,,那么 的值是 A. B. C. D. 7. 已知数列 的首项 , ,则下列结论正确的是 A. 数列 是等比数列 B. 数列 是等比数列 C. 数列 是等差数列 D. 数列 是等差数列 8. 如图,坐标纸上的每个单元格的边长为 ,由下往上有六个点:,每个点的横坐标分别对应数列 的第 项、每个点的纵坐标分别对应数列 的第 项,按如此规律下去,则 等于 A. B. C. D. 9. 在数列 中,,,则 的值为 A. B. C. D. 10. 已知数列 中,,,则 A. B. C. D. 二、填空题(共5小题;共25分) 11. 已知数列 的前 项和为 ,且 ,, 时,,则 的通项公式 . 12. 将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表: 则 = (用含 的代数式表示). 13. 已知数列 中,, 时,,则通项公式 . 14. 设 是首项为 的正项数列,且 (),则它的通项公式是 . 15. 设数列 的前 项和为 ,若 ,则 . 三、解答题(共3小题;共39分) 16. 根据下面各数列的前几项,写出该数列的一个通项公式: (1),,,, (2),,,,, (3),,,,,,,,, 17. (1)已知数列 中,,,求数列 的通项公式; (2)已知 为数列 的前 项和,,,求数列 的通项公式. 18. 设 为数列 的前 项和,且 ,数列 的通项公式为 . (1)求数列 的通项公式; (2)若将数列 与 的公共项按它们在原来数列中的先后顺序排成一个新数列 ,证明数列 的通项公式为 . 答案 第一部分 1. A 【解析】由已知,得 . 2. A 3. C 4. D 【解析】提示:. 5. D 6. D 7. A 【解析】 ,数列 是以 为公比的等比数列. 8. B 【解析】提示:这个数列的规律是奇数项为:;偶数项为:. 9. B 10. C 【解析】提示:对 两边同时取倒数,得 ,因此,数列 为首项是 ,公差是 的等差数列. 第二部分 11. 【解析】由 得, . 又 ,, 所以 . 又 , 所以 , 所以 , 所以 , 所以数列 是首项为 ,公差为 的等差数列, 所以 , 所以当 时,, 又 满足上式, 所以 . 12. 【解析】提示:剪一剪刀增加 个三角形. 13. 【解析】由 ,变形得 ,令 ,得 ,则 为以 为首项, 为公比的等比数列,所以 ,故 . 14. 【解析】由 可,,又 为正数列,所以 . 故当 时有 当 时, 满足通项公式,所以 . 15. 第三部分 16. (1) . (2) . (3) . 17. (1) 方法一:(叠加法) 因为 ,,所以 . 所以 方法二:(迭代法) 因为 ,,所以 所以 (2) 因为 ,,所以当 时,, 所以 . 所以 18. (1) 由 ,得: 当 时,, ; 当 时,, ,即 . 数列 是以 为首项,公比为 的等比数列. . (2) 由(1)知 , 显然不是数列 中的项, , 是数列 中的第 项. 设 是数列 中的第 项,则 , , 不是数列 中的项. , 是数列 中的项. . 数列 的通项公式是 . 第1页(共1 页) ... ...
~~ 您好,已阅读到文档的结尾了 ~~