2.2 探索轴对称的性质同步练习（含解析）

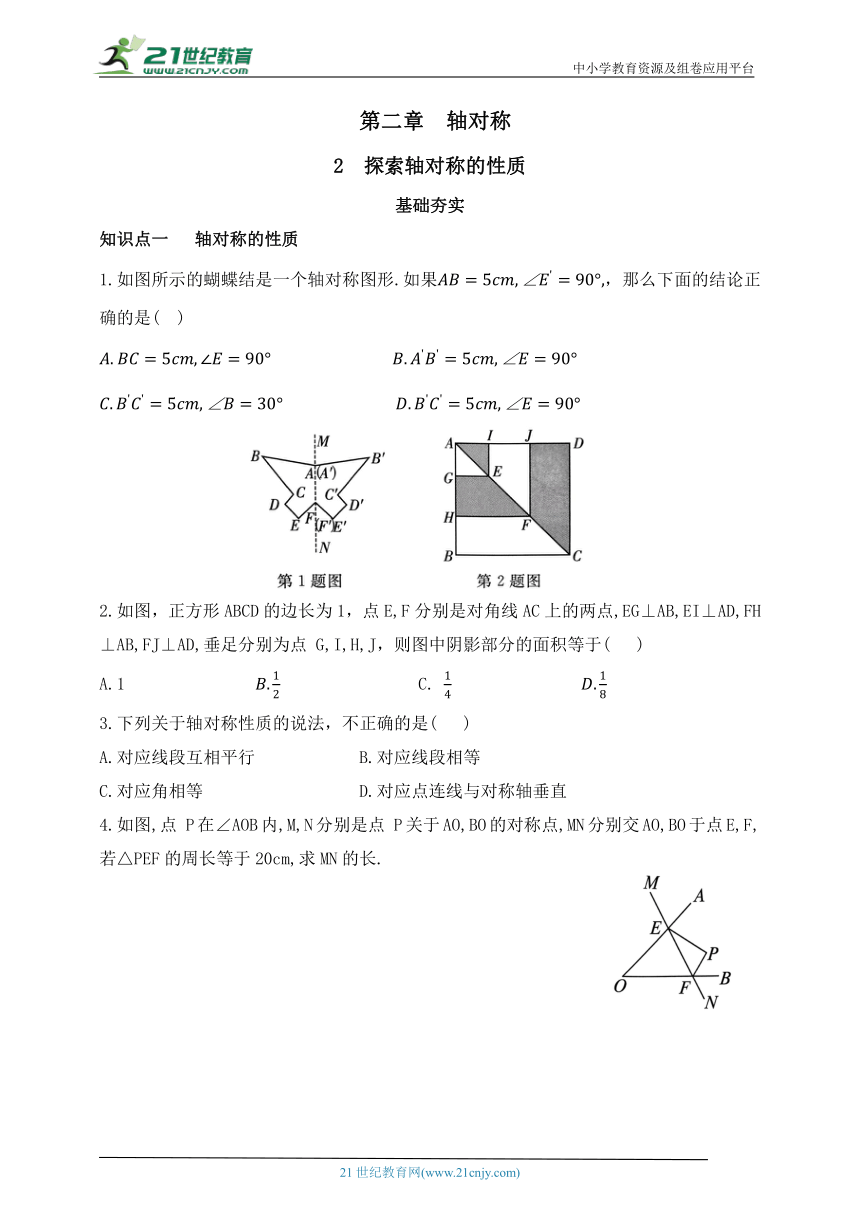
中小学教育资源及组卷应用平台 第二章 轴对称 2 探索轴对称的性质 基础夯实 知识点一 轴对称的性质 1.如图所示的蝴蝶结是一个轴对称图形.如果，那么下面的结论正确的是( ) 2.如图，正方形ABCD的边长为1，点E,F分别是对角线AC上的两点,EG⊥AB,EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为点 G,I,H,J，则图中阴影部分的面积等于( ) A.1 C. 3.下列关于轴对称性质的说法，不正确的是( ) A.对应线段互相平行 B.对应线段相等 C.对应角相等 D.对应点连线与对称轴垂直 4.如图,点 P在∠AOB内,M,N分别是点 P关于AO,BO的对称点,MN分别交AO,BO于点E,F,若△PEF的周长等于20cm,求MN的长. 知识点二 画轴对称图形 5.如图，以直线 AB为对称轴画出图形的另一半，使它成为轴对称图形. 6.画出图中的△ABC关于直线的对称图形. 易错点 想当然判断最小值 7.如图，在长度为1个单位长度的小正方形组成的正方形网格中，点 A，B，C在小正方形的顶点上. (1)在图中画出△ABC关于直线l成轴对称的 (2)在直线l上找一点P,使PB+PC的长最短，标出点 P(保留作图痕迹). 能力提升 8.如图,△ABC和 关于直线 对称，下列结论： ③垂直平分线段(④直线BC和 的交点不一定在l上.其中正确的有( ) A.4个 B.3个 C.2个 D.1个 9.如图,△ABC中,D,E,F三点分别在AB,BC,AC上,且四边形 BEFD是以DE为对称轴的轴对称图形，四边形 CFDE 是以FE为对称轴的轴对称图形.若∠C=40°，则∠DFE的度数为( ) A.65° B.70° C.75° D.80° 10.如图,在 Rt△ABC中,∠ACB=90°,点 D在AB边上,将△CBD沿CD折叠,使点 B恰好落在AC边上的点 E处.若∠A=26°,则∠CDE=_____. 11.如图,△ABC的周长为6 cm,D,E分别是AB,AC上的点,将△ADE沿直线DE折叠，点A 落在点 处,且点 A'在△ABC外部，则阴影部分图形的周长为_____cm. 12.如图,已知△ABC和 关于直线成轴对称. (1)在图中标出点 A，B，C的对称点 (2)若AB=5,则对应线段 (3)若 求∠B的度数. 核心拓展 13.如图,O为△ABC内部一点,OB=3,P,R为O分别以直线AB、直线 BC为对称轴的对称点. (1)请指出当∠ABC为多少度时,使得 PR的长度等于6 并说明理由. (2)请判断当∠ABC不是(1)中得出的角度时，PR的长度是小于6还是会大于6 并完整说明你判断的理由. 参考答案 1. B 2. B 3. A 4.解:因为M,N分别是点 P关于AO,BO的对称点,所以 ME=PE,NF=PF. 所以MN=ME+EF+FN=PE+EF+PF=△PEF的周长. 因为△PEF的周长等于 20cm,所以MN=20cm. 5.解：如图所示. 6.解:如图, 就是△ABC关于直线l的对称图形. 7.解:(1)如图,△A'B'C'为所作. (2)如图,点 P为所作. 8. B 9. D【解析】因为四边形 BEFD是以DE为对称轴的轴对称图形，四边形CFDE是以FE为对称轴的轴对称图形，所以=40°,所以∠DFE=180°-∠DEF-∠EDF=80°.故选 D. 10.71°【解析】由折叠知 所以∠CDB=∠ACD+∠A=45°+26°=71°.所以∠CDE=∠CDB=71°.故答案为71°. 11.6 【解析】利用轴对称的性质，阴影部分图形的周长=△ABC的周长.故答案为6. 12.解:(1)图略; (2)5; (3)由轴对称的性质知 所以∠B=180°-50°-20°=110°. 13.解:(1)∠ABC=90°时,PR=6. 理由:如图,连接PB,RB, 因为P，R为O分别以直线AB、直线BC为对称轴的对称点，所以PB=OB=3,RB=OB=3, ∠ABP+∠CBR=∠ABO+∠CBO=∠ABC. 因为PB+RB=PR=6,所以点P，B，R三点共线. 所以∠PBR=180°.所以∠ABC=90°. (2)PR的长度是小于6. 理由如下:∠ABC≠90°,则点P，B，R三点不在同一直线上，所以PB+BR＞PR. 因为PB+BR=2OB=2×3=6,所以PR＜6. 21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页） 21世纪教育网(www.21cnjy.com) ... ...