6.2 利用导数研究函数的性质——高二数学人教B版(2019)选择性必修第三册课时优化训练（含解析）

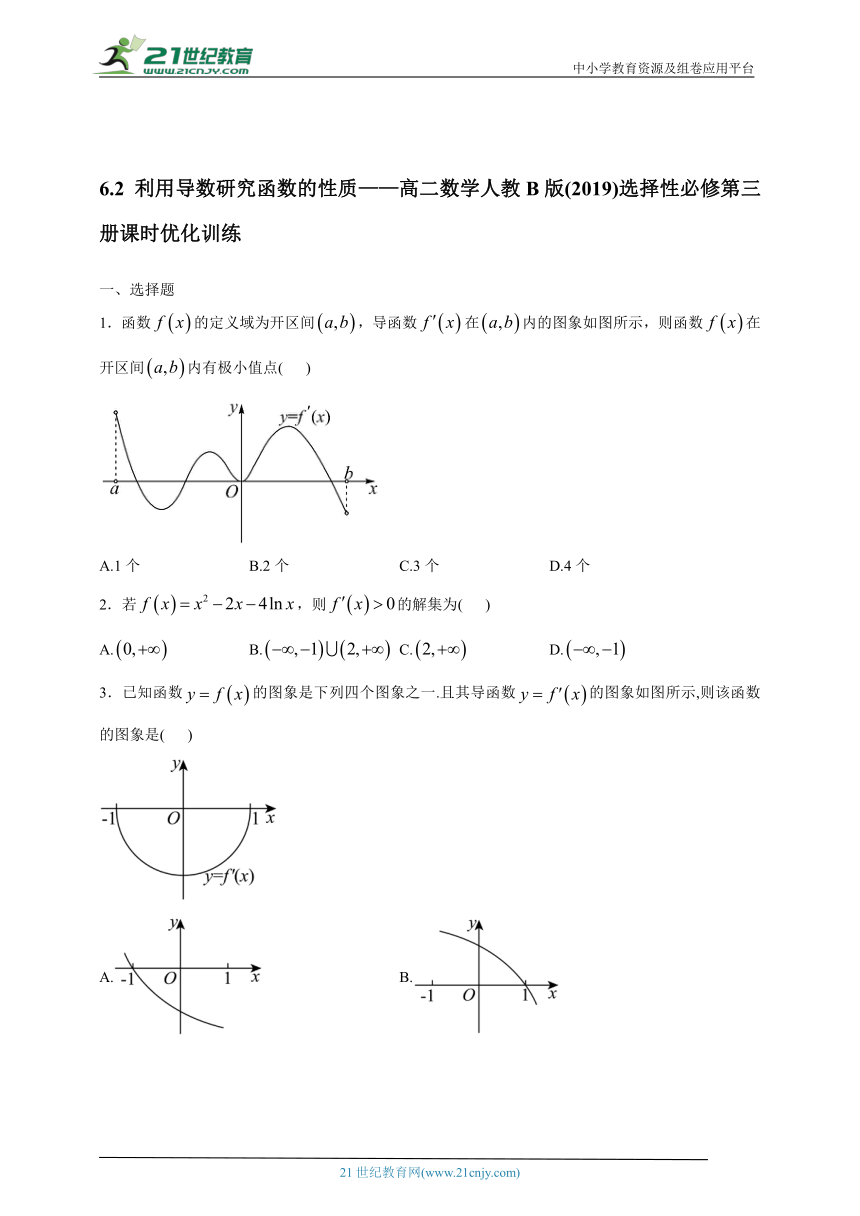
中小学教育资源及组卷应用平台 6.2 利用导数研究函数的性质———高二数学人教B版(2019)选择性必修第三册课时优化训练 一、选择题 1．函数的定义域为开区间，导函数在内的图象如图所示，则函数在开区间内有极小值点( ) A.1个 B.2个 C.3个 D.4个 2．若，则的解集为( ) A. B. C. D. 3．已知函数的图象是下列四个图象之一.且其导函数的图象如图所示,则该函数的图象是( ) A. B. C. D. 4．若函数在区间上是增函数，则实数k的取值范围为( ) A. B. C. D. 5．已知函数在定义域内可导,的大致图象如图所示,则其导函数的大致图象可能为( ) A. B. C. D. 6．设是函数的导函数，的图象如图所示，则的图象最有可能的是( ) A. B. C. D. 7．函数的图象如图所示，则不等式的解集( ) A. B. C. D. 8．在给出的①;②;③三个不等式中,正确的个数为( ) A.0个 B.1个 C.2个 D.3个 二、多项选择题 9．若函数,在区间上单调,则实数m的取值范围可以是( ) A. B. C. D. 10．函数,的导函数图象如图所示,下列结论中一定正确的是( ) A.的减区间是 B.的增区间是 C.有一个极大值点,两个极小值点 D.有三个零点 11．已知函数，其导函数的图象如图所示，则下列说法正确的是( ) A.函数在上单调递增 B.函数在上单调递减 C.函数在处取得极小值 D.函数在处取得最大值 三、填空题 12．设函数，则的单调递增区间为_____. 13．已知和分别是函数的极大值点和极小值点.若，则a的取值范围是_____. 14．函数的单调增区间是_____. 四、解答题 15．已知函数在时取得极大值4. （1）求实数a，b的值； （2）求函数在区间上的最值. 16．已知函数. （1）讨论的单调性； （2）若，函数在区间上的最大值与最小值的差为1，求m的值. 17．若函数，为函数的极值点. （1）求b的值； （2）求函数的极值. 18．已知函数 （1）若,求的增区间; （2）若,且函数存在单调递减区间,求a的取值范围; （3）若且关于x的方程在上恰有两个不相等的实数根,求实数b的取值范围. 19．已知函数. （1）讨论函数的单调性； （2）证明不等式恒成立. 参考答案 1．答案：A 解析：由导函数在区间内的图象可知，函数在内的图象与x轴有四个公共点， 在从左到右第一个交点处导数左正右负，它是极大值点；在从左到右第二个交点处导数左负右正，它是极小值点；在从左到右第三个交点处导数左正右正，它不是极值点；在从左到右第四个交点处导数左正右负，它是极大值点.所以函数在开区间内的极小值点有1个. 故选：A. 2．答案：C 解析：由得，，， 令且， 解得， 即的解集为. 故选：C. 3．答案：D 解析：图象可知,. 故函数在处,切线的斜率为0, 只有选项D满足条件. 故选：D. 4．答案：C 解析：由，可得，记，， 则，所以在单调递增，所以. 故选：C. 5．答案：A 解析：当时,单调递增,且切线的斜率在减小,则,且在单调递减, 当时,单调递增,且切线的斜率在增大,则,且在单调递增, 所以排除BCD, 故选：A. 6．答案：C 解析：根据导函数图象可知，函数在，上单调增，在上单调减，从而可得结论.解：根据导函数图象可知，函数在(上单调增，在上单调减，由此可知函数的图象在，取得极值，并且前者是极大值，后者是极小值，那么可知最有可能的是C，故选C. 7．答案：A 解析：由图可得，在上单调递增，上单调递减，上单调递增 所以当时，，当时，， 所以当时，由可得，所以， 当时，由可得，所以， 所以不等式的解集为. 故选：A. 8．答案：B 解析： 9．答案：AC 解析：定义域为,; 由得函数的增区间为; 由得函数的减区间为; 因为在区间上单调, 所以或 解得或; 结合选项可得A,C正确. 故选:AC. 10．答案：BC 解析：结合导函数图象可知,当时,,单调递减, 当时,,单调递增, 当时,,单调递减, 当时,,单调递增, 所以,函数的单调递减区间为,,单调递增区间为,,A ... ...