6.1基本立体图形（含解析）——2023-2024学年高一数学北师大版2019必修第二册同步课时训练

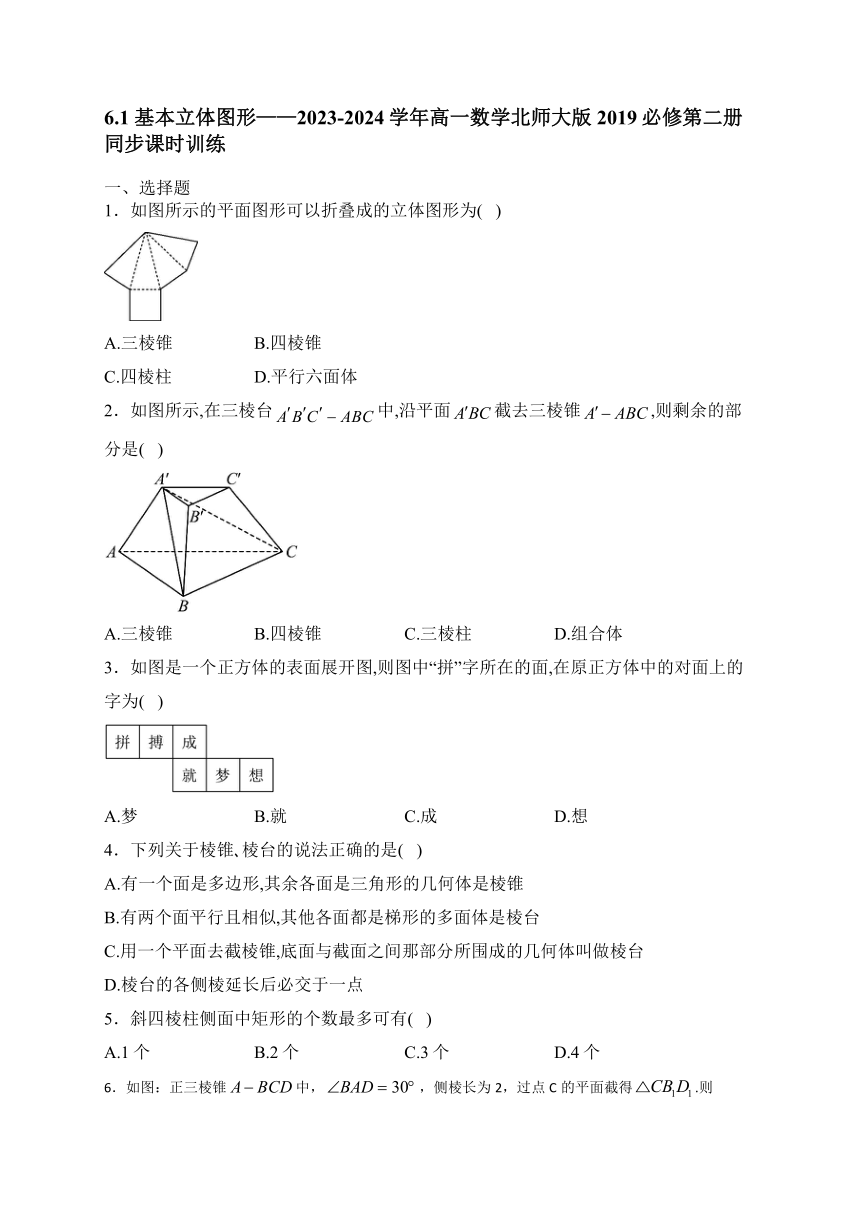
6.1 基本立体图形———2023-2024学年高一数学北师大版2019必修第二册同步课时训练 一、选择题 1．如图所示的平面图形可以折叠成的立体图形为( ) A.三棱锥 B.四棱锥 C.四棱柱 D.平行六面体 2．如图所示,在三棱台中,沿平面截去三棱锥,则剩余的部分是( ) A.三棱锥 B.四棱锥 C.三棱柱 D.组合体 3．如图是一个正方体的表面展开图,则图中“拼”字所在的面,在原正方体中的对面上的字为( ) A.梦 B.就 C.成 D.想 4．下列关于棱锥 棱台的说法正确的是( ) A.有一个面是多边形,其余各面是三角形的几何体是棱锥 B.有两个面平行且相似,其他各面都是梯形的多面体是棱台 C.用一个平面去截棱锥,底面与截面之间那部分所围成的几何体叫做棱台 D.棱台的各侧棱延长后必交于一点 5．斜四棱柱侧面中矩形的个数最多可有( ) A.1个 B.2个 C.3个 D.4个 6．如图：正三棱锥中，，侧棱长为2，过点C的平面截得.则的周长的最小值为( ) A.2 B. C.4 D. 7．一个球体被两个平行平面所截,夹在两平行平面间的部分叫做“球台”,两平行平面间的距离叫做球台的高.如图1,西晋越窑的某个“卧足杯”的外形可近似看作球台,其直观图如图2,已知杯底的直径为,杯口直径为,杯的深度为,则该卧足杯侧面所在球面的半径为( ) A. B. C. D. 8．已知H是球O的直径上一点,,平面,H为垂足,截球O所得截面的面积为,M为上的一点,且,过点M作球O的截面,则所得的截面面积最小的圆的半径为( ) A. B. C. D. 二、多项选择题 9．下列说法中不正确的是( ) A.棱柱的侧面可以是三角形 B.正方体和长方体都是特殊的四棱柱 C.所有几何体的表面都能展开成平面图形 D.棱柱的各条棱都相等 10．两平行平面截半径为5的球,若截面面积分别为和,则这两个平面间的距离是( ) A.1 B.3 C.4 D.7 11．已知棱长为1的正方体,点P是面对角线上的任一点,则的值可能是( ) A. B.2 C. D. 三、填空题 12．圆柱侧面的母线有_____条. 13．如图，已知正三棱柱的底面边长为，高为，一质点自A点出发，沿着三棱柱的侧面绕行一周到达点的最短路线的长为_____. 14．圆锥的底面半径为1,其侧面展开图是一个圆心角为的扇形,则此圆锥的母线长为_____. 四、解答题 15．下图的几何体是棱柱吗？为什么？ 16．正四棱台的高是17cm,两底面的边长分别是4cm和16cm,求这个棱台侧棱的长和斜高. 17．判断下列几何体是不是圆台,为什么 (1) (2) (3) 18．已知长方体,如图所示. 1.长方体是棱柱吗 如果是,是几棱柱 请说明理由. 2.用平面把这个长方体分成两部分,各部分还是棱柱吗 如果是,判断是几棱柱,并用符号表示;如果不是,请说明理由. 19．已知球的两个平行截面的面积分别为和，它们位于球心的同一侧，且距离为1，求这个球的半径. 参考答案 1．答案：B 解析：由展开图可知，该几何体有四个三角形面与一个四边形面，故该几何体为四棱锥； 故选：B. 2．答案：B 解析：三棱台中,沿平面截去三棱锥, 剩余的部分是以为顶点,四边形为底面的四棱锥． 故选：B. 3．答案：C 解析：根据正方体的表面展开图,翻折成正方体,如图所示： 其中“成”在最下面,“拼”在最上面,构成对面关系. 故选：C. 4．答案：D 解析：有一个面是多边形,其余各面是三角形,若其余各面没有一个共同的顶点,则不是棱锥,故A错误; 两个面平行且相似,其他各面都是梯形的多面体不一定是棱台,还要满足各侧棱的延长线交于一点,故B错误,D正确; 用一个平行于底面的平面去截棱锥,底面与截面之间那部分所围成的几何体叫做棱台,故C错误. 故选：D. 5．答案：B 解析：由于在斜四棱柱的底面中最多有两条平行的对边和侧棱垂直，其余一组对边不和侧棱垂直， 故此时四棱柱的侧面中最多有2个侧面为矩形，且这两个侧面为相对的面， 其余一组相对的侧面不可能为矩形， 故选：B 6．答案：D 解析：由题意，沿正三棱锥的侧棱A ... ...