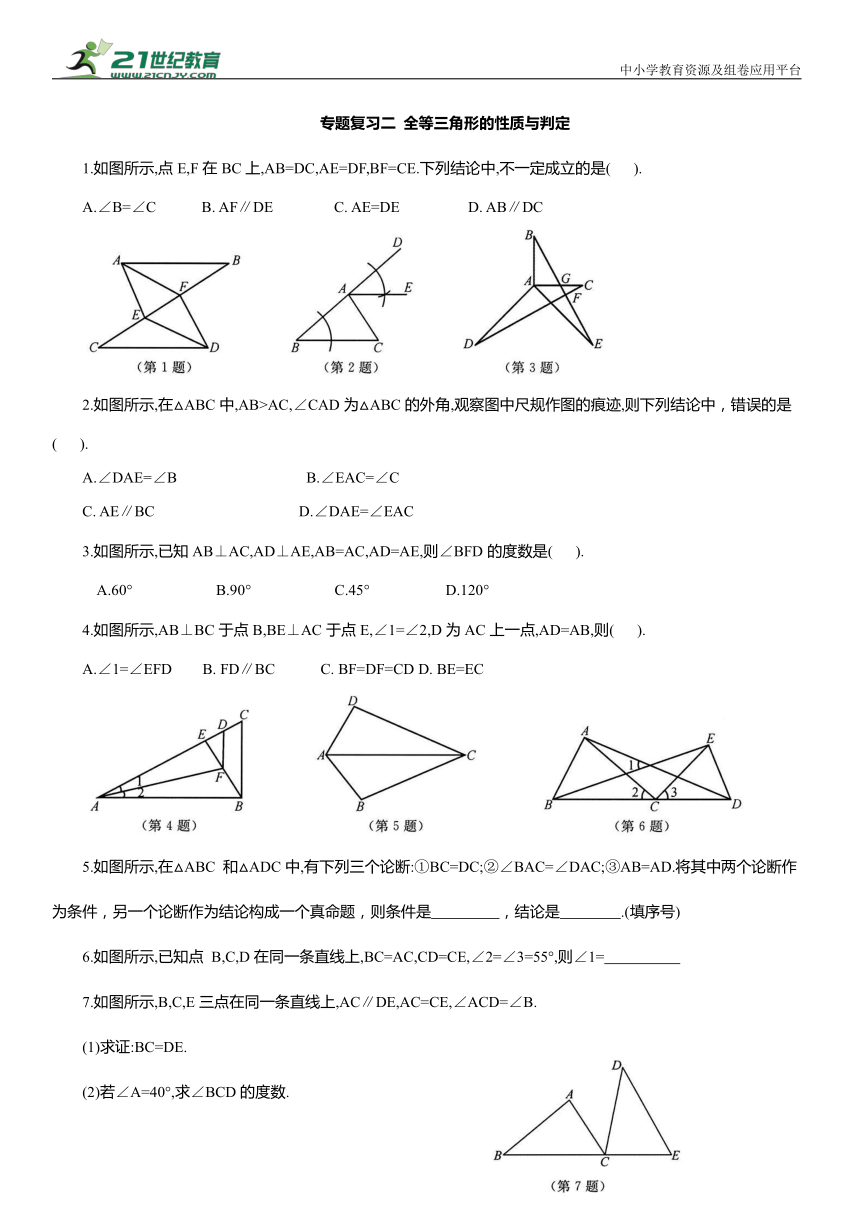
中小学教育资源及组卷应用平台 专题复习二 全等三角形的性质与判定 1.如图所示,点E,F在BC上,AB=DC,AE=DF,BF=CE.下列结论中,不一定成立的是( ). A.∠B=∠C B. AF∥DE C. AE=DE D. AB∥DC 2.如图所示,在△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论中,错误的是( ). A.∠DAE=∠B B.∠EAC=∠C C. AE∥BC D.∠DAE=∠EAC 3.如图所示,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( ). A.60° B.90° C.45° D.120° 4.如图所示,AB⊥BC于点B,BE⊥AC于点E,∠1=∠2,D为AC上一点,AD=AB,则( ). A.∠1=∠EFD B. FD∥BC C. BF=DF=CD D. BE=EC 5.如图所示,在△ABC 和△ADC中,有下列三个论断:①BC=DC;②∠BAC=∠DAC;③AB=AD.将其中两个论断作为条件,另一个论断作为结论构成一个真命题,则条件是 ,结论是 .(填序号) 6.如图所示,已知点 B,C,D在同一条直线上,BC=AC,CD=CE,∠2=∠3=55°,则∠1= 7.如图所示,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B. (1)求证:BC=DE. (2)若∠A=40°,求∠BCD的度数. 8.如图所示,OA=OB,OC=OD,∠1=∠2=∠3,AC交OB 于点M,BD交OC 于点N.求证:OM=ON. 9.如图所示,已知点E在△ABC的外部,点 D在BC边上,DE交AC 于点F,若∠1=∠2=∠3,AC=AE,则有( ). A.△ABD≌△AFD B.△AFE≌△ADC C.△AEF≌△DFC D.△ABC≌△ADE 10.在如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数为( ). A.330° B.315° C.310° D.360° 11.如图所示,在△ABC中,∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD交BD 延长线于点E,若 BD=8,则CE的长为( ). A.4 B.3 C.3.5 D.4.5 12.在△ABC中,AC=2,中线AD=3,则AB边的取值范围是 . 13.如图所示,在四边形ABCD中, 于点E,若线段AE=5,则 S四边形ABCD= . 14.如图所示,AC=BC,DC=EC,∠ACB=∠ECD=90°,且, 则∠AEB= 15.如图所示,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC 于点G.求证: (1)DF∥BC. (2)FG=FE. 16.如图所示,在△ABC中, ,BD 平分 ,交AC于点D, BD于点F,交 BC于点E.求证: (1)AB=BE. (2)AD=CE. (3)BE-CE=CD. 17.如图所示,已知在△ABD 和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是 .(填一个即可) 18. (1)如图1所示,已知CE与AB交于点 E,AC=BC,∠1=∠2.求证:△ACE≌△BCE. (2)如图2所示,已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由. 19.如图1所示,AB=4cm,AC⊥AB于点A,BD⊥AB于点B,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段 BD上由点 B 向点 D 运动.它们运动的时间为t(s). (1)若点 Q的运动速度与点 P 的运动速度相等,当t=1时,△ACP 与△BPQ是否全等 请说明理由,并判断此时线段 PC 和线段 PQ 的位置关系. (2)如图2所示,将图1中的“AC⊥AB于点A,BD⊥AB 于点 B”改为“∠CAB=∠DBA=60°”,其他条件不变.设点 Q 的运动速度为x(cm/s),是否存在实数x,使得△ACP与△BPQ全等 若存在,求出相应的x,t的值;若不存在,请说明理由. 专题复习二 全等三角形的性质与判定 1. C 2. D 3. B 4. B 5.②③ ①(答案不唯一) 6.55° 7.(1)∵AC∥DE,∴∠ACB=∠E,∠ACD=∠D.∵∠ACD=∠B,∴∠D=∠B. 在△ABC和△CDE中, ∴△ABC≌△CDE(AAS).∴BC=DE. (2)∵△ABC≌△CDE,∴∠A=∠DCE=40°. 8.∵∠1=∠3,∴∠1+∠2=∠3+∠2,即∠AOC=∠BOD. 在△AOC 和△BOD中,∴ ∴△AOC≌△BOD(SAS).∴∠OAC=∠OBD. 在△AOM 和△BON中, ∴△AOM≌△BON(ASA).∴OM=ON. 9. D 10. B 11. A 12.4