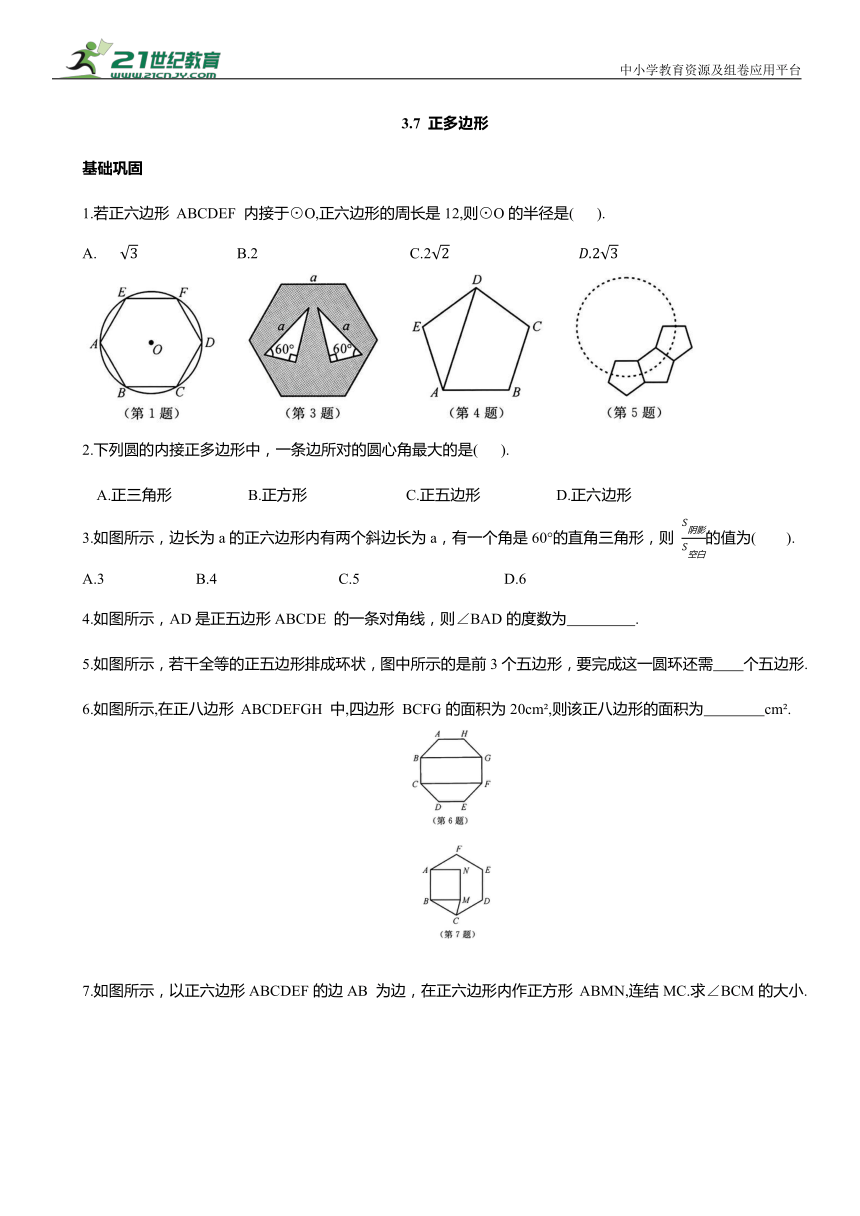
中小学教育资源及组卷应用平台 3.7 正多边形 基础巩固 1.若正六边形 ABCDEF 内接于⊙O,正六边形的周长是12,则⊙O的半径是( ). A. B.2 C.2 2.下列圆的内接正多边形中,一条边所对的圆心角最大的是( ). A.正三角形 B.正方形 C.正五边形 D.正六边形 3.如图所示,边长为a的正六边形内有两个斜边长为a,有一个角是60°的直角三角形,则 的值为( ). A.3 B.4 C.5 D.6 4.如图所示,AD是正五边形ABCDE 的一条对角线,则∠BAD的度数为 . 5.如图所示,若干全等的正五边形排成环状,图中所示的是前3个五边形,要完成这一圆环还需 个五边形. 6.如图所示,在正八边形 ABCDEFGH 中,四边形 BCFG的面积为20cm ,则该正八边形的面积为 cm . 7.如图所示,以正六边形ABCDEF的边AB 为边,在正六边形内作正方形 ABMN,连结MC.求∠BCM的大小. 能力提升 8.蜂巢的构造非常美丽、科学.如图所示为由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,△ABC 的顶点都在格点上.设定AB边如图所示,如果△ABC是直角三角形,那么这样的三角形有( ). A.4个 B.6个 C.8个 D.10个 9.如图所示,平面上有两个全等的正十边形,其中点 A 与点A'重合,点 C 与点C'重合.则∠BAJ'的度数为 . 10.如图所示,M,N分别是⊙O的内接正三角形 ABC、正方形ABCD、正五边形 ABCDE、…、正 n 边形 ABCDE…的边AB,BC上的点,且BM=CN,连结OM,ON. (1)求图1中∠MON 的度数. (2)图2中∠MON的度数为 ,图3中∠MON 的度数为 . (3)试探究∠MON 的度数与正n边形边数n的关系(直接写出答案). 11.如图1所示,已知在正五边形ABCDE中. (1)AC与BE 相交于点 P,求证:四边形 PEDC 为菱形. (2)延长CD,与AE交于点M,连结BM交CE 于点N,如图2所示,求证:CN=EP. 夯实演练 12.已知正方形 MNOK 和正六边形ABCDEF 的边长均为1,把正方形放在正六边形中,使OK 边与AB 边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点 B按顺时针方向旋转,使KM边与BC 边重合,完成第一次旋转;再绕点 C按顺时针方向旋转,使MN边与CD 边重合,完成第二次旋转……在这样连续6次旋转的过程中,点B,M之间的距离可能是( ). A.1.4 B.1.1 C.0.8 D.0.5 13.如图所示,正六边形A1A2A3A4A5A6内部有一个正五边形 且A A ∥B B ,直线l经过点B2,B3,则直线l与A1A2的夹角α的度数为 . 14.(1)如图1所示,△ABC是⊙O的内接等边三角形,P 为 上一动点,求证:PA=PB+PC. (2)如图2所示,四边形ABCD是⊙O的内接正方形,P 为上一动点,求证:PA= (3)如图3所示,六边形ABCDEF 是⊙O的内接正六边形,P 为 上一动点,请探究PA,PB,PC三者之间有何数量关系,并给予证明. 3.7 正多边形 1. B 2. A 3. C 4.72° 5.7 6.40 7.∵六边形 ABCDEF为正六边形, ∴∠ABC=120°,AB=BC. ∵四边形 ABMN 为正方形, ∴∠ABM=90°,AB=BM. ∴∠BCM=∠BMC=75°. 8. D 9.108° 10.(1)连结OB,OC.∵AB=AC,∴∠ABC=∠ACB. ∵OC=OB,点O是外接圆的圆心, ∴BO平分∠ABC,CO平分∠ACB. ∴∠OBM=∠OCN=30°. ∵BM=CN,OC=OB,∴△OMB≌△ONC. ∴∠BOM=∠NOC.∴∠MON=∠BOC. ∵∠BAC=60°,∴∠BOC=120°.∴∠MON=120°. (2)90° 72° 11.(1)∵五边形 ABCDE是正五边形, ∴∠BCD=∠BAE=108°,CD=DE=BC=AB=AE. ∴∠ABE=∠AEB=36°.∴∠CBE=72°. ∴∠DCB+∠CBE=180°.∴CD∥BE. 同理可证AC∥DE,∴四边形 PEDC是平行四边形. 又∵CD=DE,∴四边形 PEDC是菱形. (2)如答图所示,连结AN. 由(1)知四边形 PEDC是平行四边形. ∵∠MCA=∠MAC=72°,∴MC=MA. ∵BC=BA,∴BM垂直平分线段AC. ∴NC=NA.∴∠NCA=∠NAC=36°. 易知∠PAE=∠NEA=72°, ∴∠PEA=∠NAE=36°. ∵AE=EA,∴△PAE≌△NEA. ∴PE=AN.∴CN=PE. 12. C 【解析】如答图所示,在这样连续 6 次旋转的过程中,点 M 的运动轨迹是图中的 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

