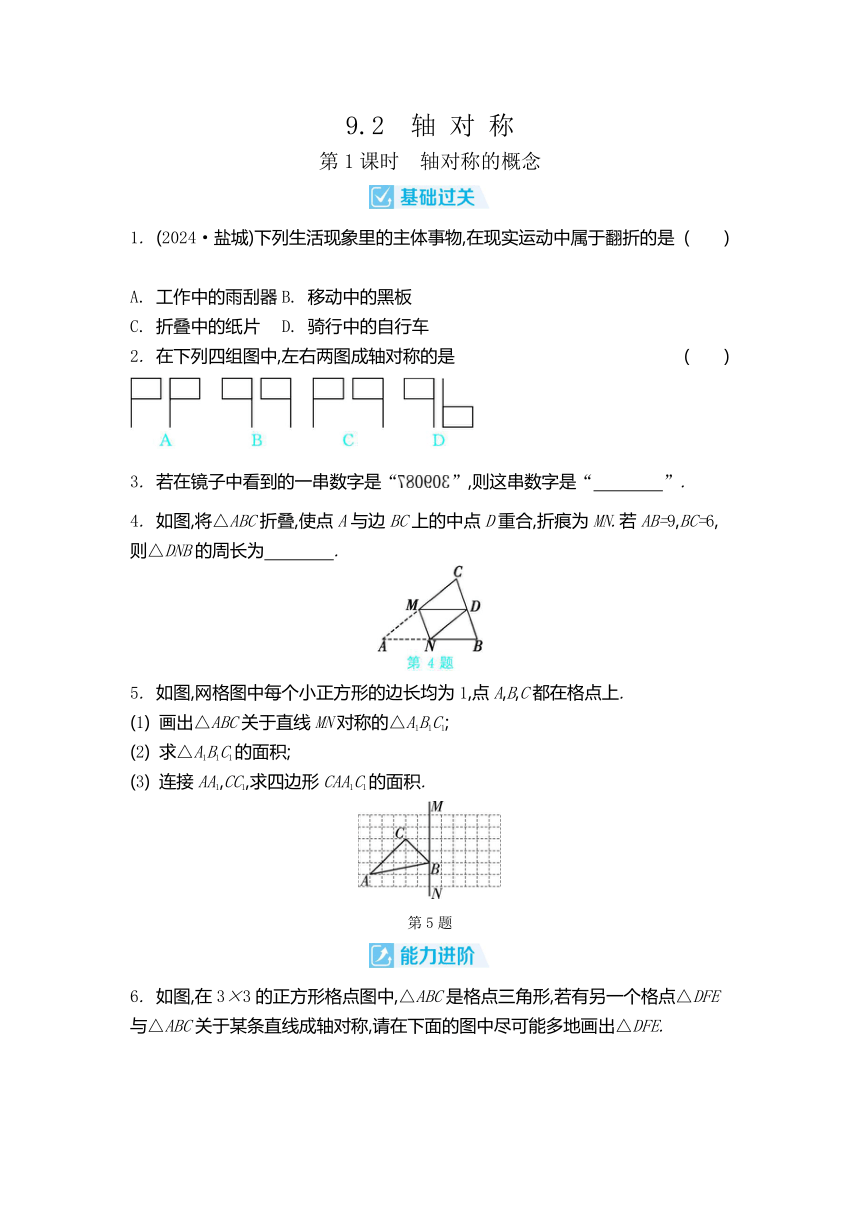
9.2 轴 对 称 第1课时 轴对称的概念 1. (2024·盐城)下列生活现象里的主体事物,在现实运动中属于翻折的是 ( ) A. 工作中的雨刮器 B. 移动中的黑板 C. 折叠中的纸片 D. 骑行中的自行车 2. 在下列四组图中,左右两图成轴对称的是 ( ) 3. 若在镜子中看到的一串数字是“”,则这串数字是“ �———�. 4. 如图,将△ABC折叠,使点A与边BC上的中点D重合,折痕为MN.若AB=9,BC=6,则△DNB的周长为 . 5. 如图,网格图中每个小正方形的边长均为1,点A,B,C都在格点上. (1) 画出△ABC关于直线MN对称的△A1B1C1; (2) 求△A1B1C1的面积; (3) 连接AA1,CC1,求四边形CAA1C1的面积. 第5题 6. 如图,在3×3的正方形格点图中,△ABC是格点三角形,若有另一个格点△DFE与△ABC关于某条直线成轴对称,请在下面的图中尽可能多地画出△DFE. 第2课时 垂直平分线的概念及其作法 1. 如图,线段AB=6,利用尺规作AB的垂直平分线,步骤如下:① 分别以点A,B为圆心,b的长为半径作弧,两弧相交于点C,D;② 作直线CD.直线CD就是线段AB的垂直平分线.由此可知,b的长可能是 ( ) A. 1 B. 2 C. 3 D. 4 2. (2024·河北改编)如图,观察尺规作图的痕迹,可得线段BD与AC的位置关系为 . 3. 如图,△ACB中,∠ACB=90°,根据图中尺规作图的痕迹填空: (1) 若AO=3,则AB的长为 ; (2) △AOF与 成轴对称; (3) 若∠A=30°,则∠FBC= °. 4. 如图,AC是长方形ABCD的对角线. (1) (2024·广元)用直尺和圆规作AC的垂直平分线,交CD于点E,交AB于点F; (2) 连接AE,CF,通过度量,图中与AE相等的线段是 . 5. 如图,在△ABC中,∠ABC为钝角.利用直尺和圆规作图: (1) 作边AC的中点D; (2) 作过点D且垂直于AB所在直线的直线DE,垂足为E. 第3课时 轴对称的基本性质 1. 下列图形中,分别以直线l为对称轴画成轴对称的图形,其中,错误的是 ( ) 2. 有下列说法:① 能够完全重合的两个图形一定成轴对称;② 成轴对称的两个图形一定能够完全重合;③ 成轴对称的两个图形的对称点一定在对称轴的两侧;④ 若点A,B关于直线MN对称,则直线MN垂直平分线段AB.其中,正确的有 ( ) A. 1个 B. 2个 C. 3个 D. 4个 3. 如图,五边形ABCDE的一个顶点E在直线l上.若要画出这个五边形关于直线l对称的图形,则最少还应确定 个点的对称点. 4. 如图,△ABC与△DEF关于直线l对称.若连接BE,则直线l是BE的 ;若再连接AD,则AD与BE的位置关系是 . 5. 如图,在图中分别标出点A,B,C关于直线l的对称点D,E,F. (1) 若M为AB的中点,在图中标出它关于直线l的对称点N; (2) 若AB=5,边AB上的高为4,则△DEF的面积为 . 6. 如图,以直线l为对称轴,画出图形的另一半. 7. (2024·河北)如图,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A,B的对称点分别是C,D.下列结论不一定正确的是 ( ) A. AD⊥BC B. 若连接AC,则AC⊥PQ C. △ABO与△CDO能完全重合 D. 若连接AC,BD,则AC∥BD 8. 如图,有一个英语单词,四个字母都关于直线l对称.若补全字母,则这个单词所指的物品是 . 9. 如图,直线l1⊥l2,分别画出线段MN关于直线l1和l2的对称线段M1N1和M2N2,则线段M1N1和M2N2 (填“成”或“不成”)轴对称. 10. 如图,△ABC的顶点C在直线l上,用直尺和圆规作△ABC关于直线l对称的△EDC. 11. 已知△ABC与△A'B'C'关于直线MN对称,△A'B'C'与△A″B″C″关于直线EF对称,△A'B'C',△A″B″C″如图所示. (1) 画出△ABC; (2) 利用尺规作出直线EF; (3) 若直线MN和EF相交于点O,直线MN和EF所夹的锐角为∠α,则∠BOB″与∠α之间的数量关系为 . 第4课时 轴对称图形 1. (2024·赤峰)在下列四个标志中,属于轴对称图形的是 ( ) 2. (2023 ... ...
~~ 您好,已阅读到文档的结尾了 ~~