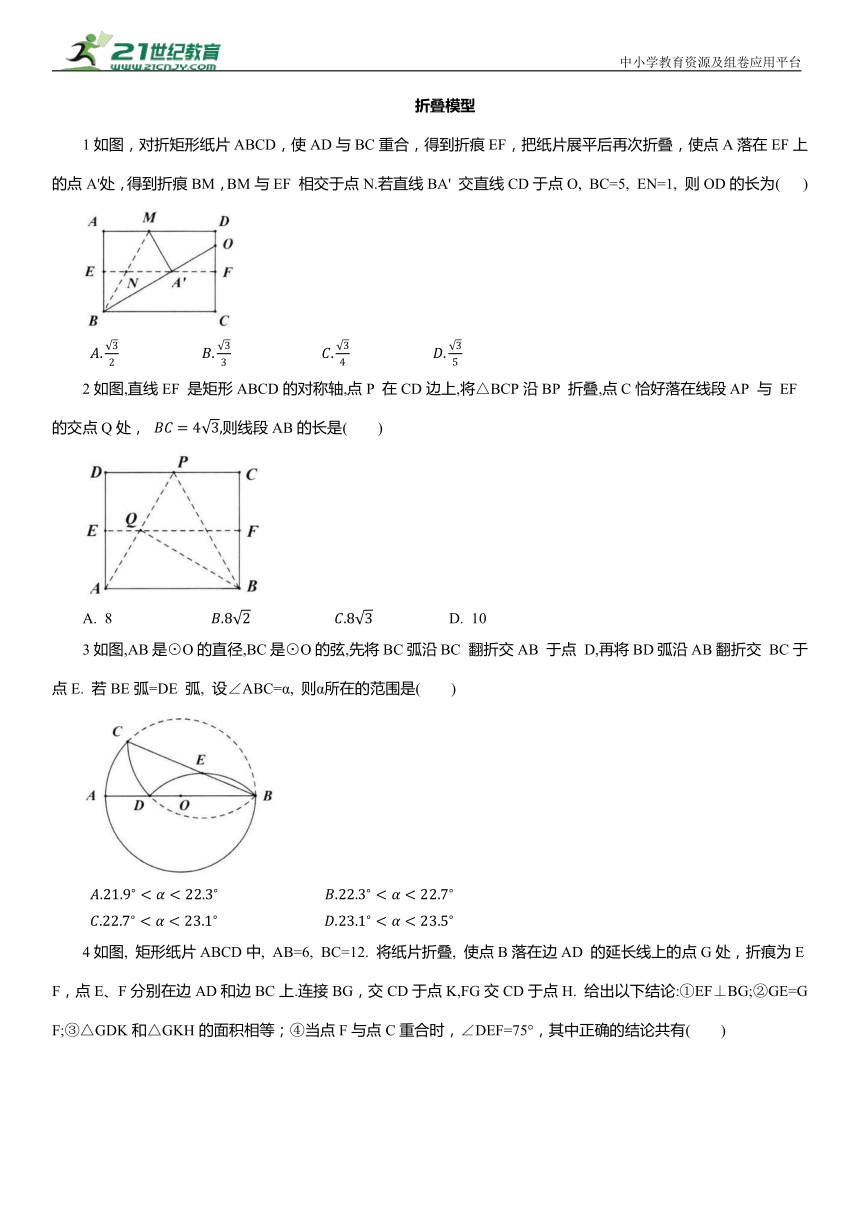
折叠模型 1如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A'处,得到折痕BM,BM与EF 相交于点N.若直线BA' 交直线CD于点O, BC=5, EN=1, 则OD的长为( ) 2如图,直线EF 是矩形ABCD的对称轴,点P 在CD边上,将△BCP沿BP 折叠,点C恰好落在线段AP 与 EF 的交点Q处, 则线段AB的长是( ) A. 8 D. 10 3如图,AB是⊙O的直径,BC是⊙O的弦,先将BC弧沿BC 翻折交AB 于点 D,再将BD弧沿AB翻折交 BC于点E. 若BE弧=DE 弧, 设∠ABC=α, 则α所在的范围是( ) 4如图, 矩形纸片ABCD中, AB=6, BC=12. 将纸片折叠, 使点B落在边AD 的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H. 给出以下结论:①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°,其中正确的结论共有( ) A. 1个 B. 2个 C. 3个 D. 4个 5如图,三角形纸片ABC,点D 是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点 F. 若DG=GE,AF=3,BF=2,△ADG的面积为2,则点F到BC的距离为 ( ) 6如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC',DC'与AB交于点E,连接AC',若AD=AC'=2,BD=3,则点D到BC'的距离为( ) 7如图, 矩形纸片ABCD, AB=4, BC=3, 点P在BC边上, 将△CDP沿DP折叠, 点C落在点E处, PE、DE分别交AB于点O、F,且OP=OF,则 cos∠ADF的值为( ) 8如图所示,在矩形纸片ABCD 中, 点E、F分别是矩形的边AD、BC上的动点,将该纸片沿直线EF折叠.使点B落在矩形边AD上,对应点记为点G, 点A 落在M处, 连接EF、BG、BE, EF与BG交于点N. 则下列结论: ①BN=AB; ②当点G与点D 重合时, ③△GNF 的面积S的取值范围是 ④当 时, 其中成立的是 ( ) A. ①③ B. ③④ C. ②③ D. ②④ 9如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF 与AC交于点O.若AE=5, BF=3, 则AO的长为( ) 10将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D 都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则 的值为( ) D. 11如图, 在Rt△ABC中, ∠BAC=90°, ∠B=36°, AD是斜边BC上的中线, 将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( ) A. 120° B. 108° C. 72° D. 36° 12如图,已知正方形ABCD的边长为1,点E、F分别在边 AD、BC上,将正方形沿着 EF 翻折,点B 恰好落在 CD边上的点 处,如 果四边形A BFE与 四边形E FCD的面积比为3:5,那么线段FC 的长为 . 13如图,矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF 所在直线折叠,使点A落在BD上的点M处, 点C落在BD上的点N处, 连接EF. 已知AB=3,BC=4,则EF 的长为 ( ) A. 3 B. 5 14如图, DE 平分等边△ABC的面积, 折叠△BDE得到△FDE, AC 分别与DF,EF 相交于G, H两点. 若DG=m, EH=n, 用含m, n的式子表示GH的长是 . 15如图,在△ABC中, AB=4, BC=7, ∠B=60°, 点D在边BC上, CD=3, 连接AD.如果将△ACD沿直线AD翻折后,点C的对应点为点E,那么点E到直线BD的距离为 . 16如图,在矩形ABCD中, E、F分别是边BC、CD上一点, 将 沿EF翻折得 连接 当 时, 是以A E为腰的等腰三角形. 17如图,在 中, 点E在线段AC上,且AE=1,D 是线段BC上的一点,连接DE,将四边形ABDE 沿直线DE 翻折,得到四边形FGDE, 当点G恰好落在线段AC上时, AF= . 18如图,在矩形ABCD中, AD=4, 将∠A向内翻折, 点A落在BC上, 记为A , 折痕为DE.若将∠B沿 向内翻折,点B恰好落在DE上,记为B ,则AB= . 19在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;第二步:将图①中的矩形纸片折叠,使点C恰好落在点F ... ...
~~ 您好,已阅读到文档的结尾了 ~~