云南省玉溪市峨山县第一中学2024-2025学年高一下学期3月份考试数学试卷（含答案）

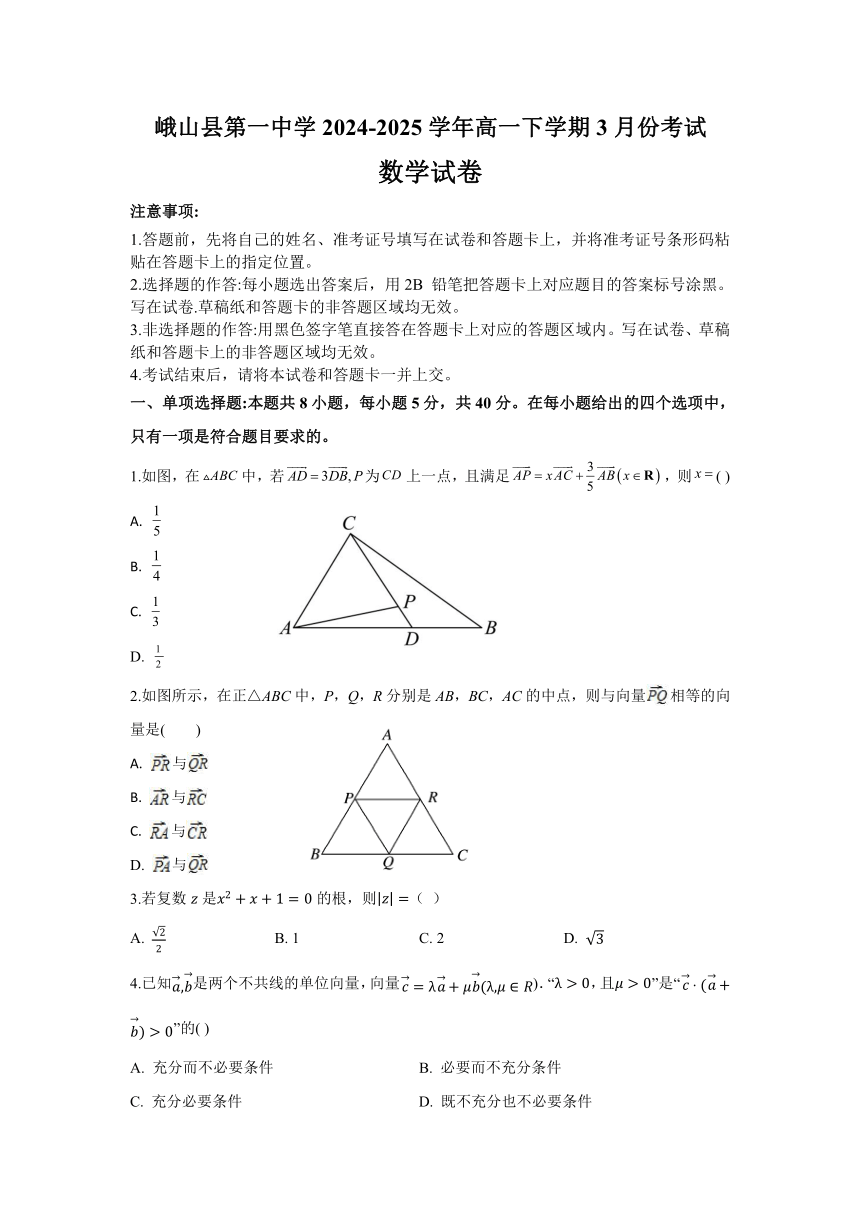
峨山县第一中学2024-2025学年高一下学期3月份考试 数学试卷 注意事项: 1.答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。 2.选择题的作答:每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。写在试卷.草稿纸和答题卡的非答题区域均无效。 3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。写在试卷、草稿纸和答题卡上的非答题区域均无效。 4.考试结束后，请将本试卷和答题卡一并上交。 一、单项选择题:本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。 1.如图，在中，若为上一点，且满足，则( ) D. 2.如图所示，在正△ABC中，P，Q，R分别是AB，BC，AC的中点，则与向量相等的向量是(　　) 与 与 与 D. 与 3.若复数是的根，则（ ） A. B. 1 C. 2 D. 4.已知是两个不共线的单位向量，向量)．“，且”是“”的( ) A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 5.在△ABC中，已知b2＝ac且c＝2a，则cos B等于(　　) A. B. C. D. 6.若是内一点，，则是的( ) A. 内心 B. 外心 C. 垂心 D. 重心 7.若，且是纯虚数，则（ ） A. B. 1 C. D. 2 8.已知A(0,1)，B(3,5)，向量a＝，b＝(sin α，cos α)，且a∥b，则tan α等于(　　) A. B. － C. D. － 二、多项选择题:本题共3小题，每小题6分，共18分。在每小题给出的四个选项中，有多项符合题目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分。 9.化简以下各式，结果为的有( ) A. B. C. D. 10.如图，在平行四边形中，分别是边上的两个三等分点，则下列选项正确的有( ). A. B. C. D. 11.设非零向量，满足，，则( ) A. B. C. D. 三、填空题:本题共3小题，每小题5分，共15分。 12.如图，，都是边长为1的等边三角形，，，三点共线，则 ． 13.若△ABC的三边长分别为AB＝7，BC＝5，CA＝6，则·＝_____. 14.已知、、为圆上的三点，若，则与夹角的大小为 . 四、解答题:本题共5 小题，其中第 15 题 13 分，第 16、17 题 15 分,第18、19题17分，共77分。解答应写出文字说明、证明过程或演算步骤。 15.已知，，分别为三个内角，，的对边，且. (1)求角； (2)若点满足，且，求的面积的最大值. 16.求实数m的值或取值范围，使得复数分别满足： (1)z是实数； (2)z是纯虚数； (3)z在复平面中对应的点位于第三象限. 17.若定义一种运算：.已知为复数，且. (1)求复数； (2)设为实数，若为纯虚数，求的最大值. 18.已知幂函数（）定义域上不单调． （1）试问：函数是否具有奇偶性？请说明理由； （2）若，求实数的取值范围． 19.英国数学家泰勒发现了如下公式：，其中，此公式有广泛的用途，例如利用公式得到一些不等式：当时，，，（解答本题时，这些不等式根据需要可以直接使用）． （1）证明：当时，； （2）设，若区间满足：当定义域为时，值域也为，则称区间为的“和谐区间”．试问是否存在“和谐区间”？若存在，求出的所有“和谐区间”，若不存在，请说明理由． 一、单选题 1.【答案】A 【解析】因为所以 由, 因三点共线，由共线定理推论可得，解得 故选：A. 2.【答案】B 【解析】由已知可得PQ AC，向量相等要求模相等，方向相同，因此与都是和相等的向量． 3.【答案】B 【解析】由复数求根公式，有，所以. 故选：B. 4.【答案】A 【解析】当，且时， ，充分性满足； 当时， ，当，时， 是可以大于零的， 即当时，可能有，，必要性不满足， 故“，且”是“”的充分而不必要条件. 故选：A. 5.【答案】B 【解析】∵b2＝ac，c＝2a，∴b2＝2a2， ∴cos B＝＝＝. 6.【答案】D 【解析】取线段的中点，连接，则，而， 因此，即三点共线， ... ...