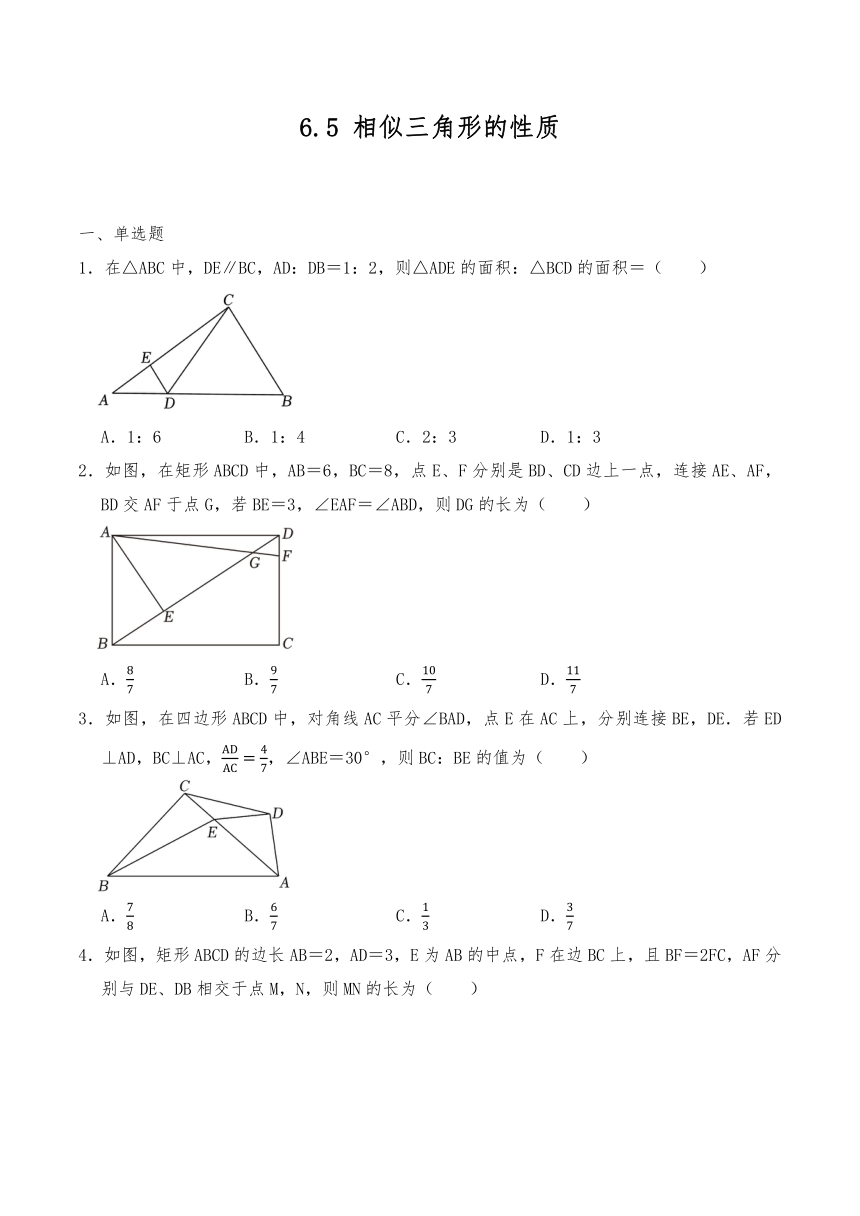
6.5 相似三角形的性质 一、单选题 1.在△ABC中,DE∥BC,AD:DB=1:2,则△ADE的面积:△BCD的面积=( ) A.1:6 B.1:4 C.2:3 D.1:3 2.如图,在矩形ABCD中,AB=6,BC=8,点E、F分别是BD、CD边上一点,连接AE、AF,BD交AF于点G,若BE=3,∠EAF=∠ABD,则DG的长为( ) A. B. C. D. 3.如图,在四边形ABCD中,对角线AC平分∠BAD,点E在AC上,分别连接BE,DE.若ED⊥AD,BC⊥AC,,∠ABE=30°,则BC:BE的值为( ) A. B. C. D. 4.如图,矩形ABCD的边长AB=2,AD=3,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( ) A. B. C. D. 5.如图,菱形ABCD的边长为3,∠ADC=60°,过点D作DE⊥AB,交BA的延长线于点E,连结CE分别交BD,AD于点G,F,则FG的长为( ) A. B. C. D. 二、填空题 6.如图,AB与CD交于点O,且AC∥BD.若,则 . 7.如图,在△ABC中,DE∥BC,联结BE,如果△ADE和△BEC的面积都为1,则△DEB的面积为 . 8.如图,菱形ABCD的边长为3,∠ADC=60°,过点D作DE⊥AB,交BA的延长线于点E,连结CE分别交BD,AD于点G,F,则FG的长为 . 9.如图,在Rt△ABC中,∠BAC=90°,BD是△ABC的一条角平分线,过点A作AE⊥BC交BC于点E,交BD于点F.若,△AFD的面积为 ,则BE= . 10.如图,点C是以AB为直径的半圆上的三等分点(BC<AC),点E为上一动点,(不与点A、C重合),过点B作BF⊥AB与EC的延长线交于点F,过点B作BG⊥OC于点G,交EC于点H,若OG=2,H为CE的三等分点,EH的长为 . 11.如图,在矩形ABCD中,AB=8,AD=4,连接AC,点E,F分别在边AD,CD上,连接BE,BF分别交AC于点M,N.若∠EBF=45°,CF=2,则DE的长为 . 三、解答题 12.如图,在菱形ABCD中,过D作DE⊥BC交BC的延长线于点E,过E作EF⊥AB交AB于点F. (1)求证△DEC∽△EFB; (2)若BC=6,CE=2,求AF的长. 13.如图,已知AB是⊙O的直径,点C是的中点,点D是的中点,连接AC,BC,AD,AD与BC交于点E,过点D作DF⊥AC于点F. (1)求证:DF为⊙O的切线; (2)若,求AD的长度. 14.如图,矩形EFGD的边EF在△ABC的边BC边上,顶点D、G分别在边AB、AC上,已知AB=AC=10,BC=12. (1)当矩形EFGD为正方形时,求正方形的边长; (2)联结EG,当△GEC以GC为腰的等腰三角形时,求矩形EFGD的面积. 15.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.有一点到终点运动即停止.问: (1)几秒后△PBQ的面积等于5; (2)几秒后PQ⊥DQ. 16.如图,在Rt△ABC中,∠ACB=90°,D是BC上一点,过点C作CE⊥AD,垂足为E.连接BE并延长交AC于点F. (1)求证:CD2=ED AD; (2)已知D为BC的中点,求证:∠DBE=∠DAB. 17.如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N. (1)求证:△ABM∽△EFA; (2)若AB=8,BM=6,求AE的长. 18.如图,在△ABC和△ADE中,AB=mAC,AD=mAE(m>1),∠BAC=∠DAE,连接BD,CE交于点O.求证: (1)△ABD∽△ACE; (2)∠BAC=∠BOC. 19.如图,在中,,为延长线上一点,,,过作,交的延长线于点. (1)求证:. (2)求长度. 20.如图,平分,. (1)求证:; (2)若,,求的长. 参考答案 一、单选题 1. 【分析】由AD:DB=1:2,推导出,由DE∥BC证明△ADE∽△ABC,得,则()2,求得S△ADC=3,S△ABC=9,所以S△BCD=6,于是得到问题的答案. 【解答】解:∵AD:DB=1:2, ∴, ∵DE∥BC,△ADE的面积为1, ∴△ADE∽△ABC, ∴, ∴, ∴S△ADC=3S△ADE= ... ...
~~ 您好,已阅读到文档的结尾了 ~~