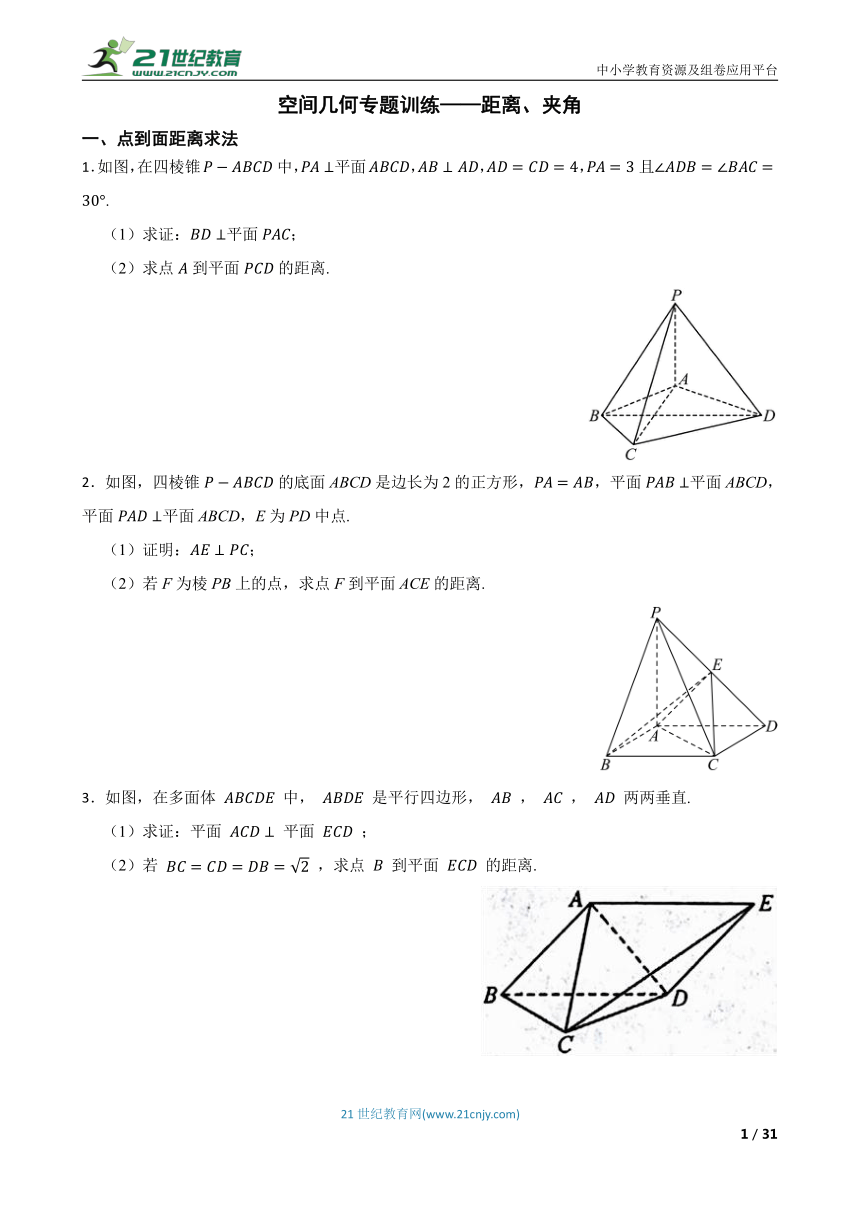
中小学教育资源及组卷应用平台 空间几何专题训练———距离、夹角 一、点到面距离求法 1.如图,在四棱锥中,平面,,,且. (1)求证:平面; (2)求点到平面的距离. 2.如图,四棱锥的底面ABCD是边长为2的正方形,,平面平面ABCD,平面平面ABCD,E为PD中点. (1)证明:; (2)若F为棱PB上的点,求点F到平面ACE的距离. 3.如图,在多面体 中, 是平行四边形, , , 两两垂直. (1)求证:平面 平面 ; (2)若 ,求点 到平面 的距离. 4.如图,在四棱锥中,底面为平行四边形,,,,,,为棱的中点. 条件①:; 条件②:平面平面. 从条件①和条件②这两个条件中选择一个作为已知,完成下列问题: (1)求证:; (2)若点在线段上,且点到平面的距离为,求线段的长. 注:如果选择条件①和条件②分别解答,按第一个解答计分. 二、异面直线夹角求法 5.如图,直三棱柱 中,所有棱长均为1,点 为棱 上任意一点,则下列结论正确的是( ) A.直线 与直线 所成角的范围是 B.在棱 上存在一点 ,使 平面 C.若 为棱 的中点,则平面 截三棱柱 所得截面面积为 D.若 为棱 上的动点,则三棱锥 体积的最大值为 6.如图,在侧棱垂直于底面的三棱柱 中, , , ,F分别是 , 的中点,则异面直线 与 所成角的余弦值是 . 7.在三棱柱 中, , .若 , ,则异面直线 与 所成的角为 . 8.如图,四棱锥 中,底面 为矩形, 底面 , , , 分别为棱 的中点. (1)求证: 、 、 、 四点共面; (2)求异面直线 与 所成的角. 三、线面夹角求法 9.如图,在三棱锥 中,侧面 底面BCD, , , , ,直线AC与底面BCD所成角的大小为 A. B. C. D. 10.如图,在四棱锥 中, , , . , 为等边三角形,点 是棱 上的一动点. (1)求证: ; (2)求直线 与平面 所成角的正弦值的最大值. 11.如图, 中, , 是边长为 的 若 , 分别是 , 的中点. (1)求证: ; (2)求证: ; (3)求 和面 所成角的大小. 四、二面角求法 12.如图,在三棱锥中,侧面是正三角形,且垂直于底面,,, (1)求证: (2)记二面角的平面角为,求的值. 13.如图,边长为2的正方形 所在的平面与半圆弧 所在平面垂直, 是 上异于 , 的点. (1)证明: ; (2)当三棱锥 体积最大时,求面 与面 所成二面角的正弦值. 14.如图所示的几何体由等高的 个圆柱和 个圆柱拼接而成,点 为弧 的中点,且 、 、 、 四点共面. (1)证明: 平面 . (2)若直线 与平面 所成角为 ,求平面 与平面 所成锐二面角的余弦值. 15.如图,在四棱锥 的展开图中,点 分别对应点 , , , ,已知 , 均在线段 上,且 , ,四边形 为等腰梯形, , . (1)若 为线段 的中点,证明: 平面 . (2)求二面角 的余弦值. 16.如图,三棱锥 中,侧棱 底面 点在以 为直径的圆上. (1)若 ,且 为 的中点,证明: ; (2)若 求二面角 的大小. 17.现有两个全等的等腰直角三角板,直角边长为2,将它们的一直角边重合,若将其中一个三角板沿直角边折起形成三棱锥 ,如图所示,其中 ,点E,F,G分别是 的中点. (1)求证: 平面 ; (2)求二面角 的余弦值. 18.如图,矩形 中, , ,点 是 上的动点.现将矩形 沿着对角线 折成二面角 ,使得 . (Ⅰ)求证:当 时, ; (Ⅱ)试求 的长,使得二面角 的大小为 . 19.如图,四棱锥 中,四边形 是等腰梯形, . (1)证明:平面 平面 ; (2)过 的平面交 于点 若平面 把四棱锥 分成体积相等的两部分,求平面 与平面 所成锐二面角的余弦值. 20.如图,在四棱锥 中, , , ,且 , , . (1)若 为 的中点,证明: ; (2)求证: ; (3)若 为 的中点,求二面角 的平面角的大小. 答案解析部分 1.【答案】(1) 由于,, 所以故 ... ...
~~ 您好,已阅读到文档的结尾了 ~~