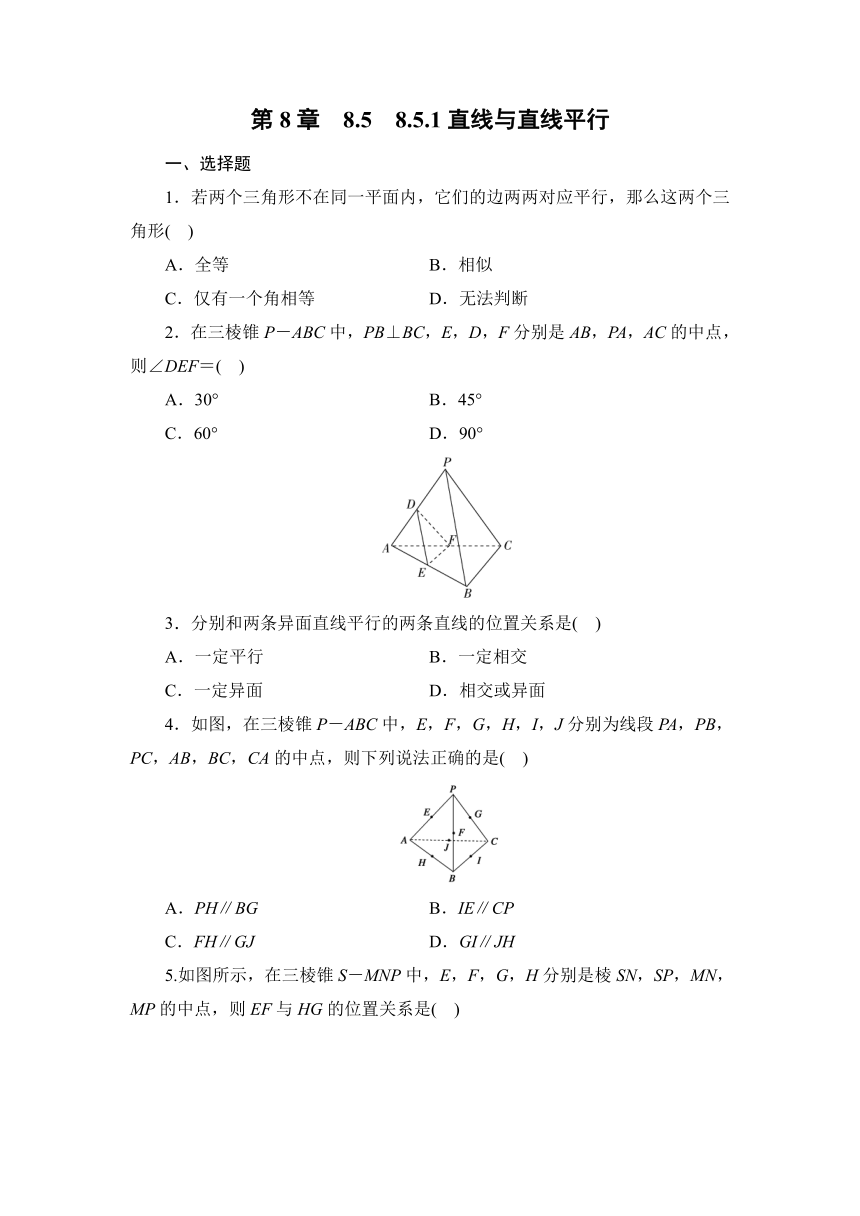
第8章 8.5 8.5.1直线与直线平行 一、选择题 1.若两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( ) A.全等 B.相似 C.仅有一个角相等 D.无法判断 2.在三棱锥P-ABC中,PB⊥BC,E,D,F分别是AB,PA,AC的中点,则∠DEF=( ) A.30° B.45° C.60° D.90° 3.分别和两条异面直线平行的两条直线的位置关系是( ) A.一定平行 B.一定相交 C.一定异面 D.相交或异面 4.如图,在三棱锥P-ABC中,E,F,G,H,I,J分别为线段PA,PB,PC,AB,BC,CA的中点,则下列说法正确的是( ) A.PH∥BG B.IE∥CP C.FH∥GJ D.GI∥JH 5.如图所示,在三棱锥S-MNP中,E,F,G,H分别是棱SN,SP,MN,MP的中点,则EF与HG的位置关系是( ) A.平行 B.相交 C.异面 D.平行或异面 6.在正方体ABCD-A1B1C1D1中,E,F分别是平面AA1D1D、平面CC1D1D的中心,G,H分别是棱AB,BC的中点,则直线EF与直线GH的位置关系是( ) A.相交 B.异面 C.平行 D.垂直 7.(多选题)下列四面体中,直线EF与MN不可能平行的是( ) 8.(多选题)如图,在四面体A-BCD中,M,N,P,Q,E分别是AB,BC,CD,AD,AC的中点,则下列说法中正确的是( ) A.M,N,P,Q四点共面 B.∠QME=∠CBD C.△BCD∽△MEQ D.四边形MNPQ为梯形 二、填空题 9.如图,AA′是长方体ABCD-A′B′C′D′的一条棱,那么长方体中与AA′平行的棱共有 条. 10.已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点,若==,==,则四边形EFGH形状为___. 11.如图,在空间四边形ABCD中,M,N分别是△ABC和△ACD的重心,若BD=m,则MN= . 12.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论: ①AB∥CM; ②EF与MN是异面直线; ③MN∥CD. 以上结论中正确结论的序号为___. 13.a,b,c是空间中的三条直线,下面给出四个命题: ①若a∥b,b∥c,则a∥c; ②若a与b相交,b与c相交,则a与c相交; ③若a 平面α,b 平面β,则a,b一定是异面直线; ④若a,b与c成等角,则a∥b. 其中正确的命题是___(填序号). 三、解答题 14.如图所示,在空间四边形ABCD(不共面的四边形称为空间四边形)中,E,F,G,H分别为AB,BC,CD,DA的中点. (1)求证:四边形EFGH是平行四边形; (2)如果AC=BD,求证:四边形EFGH是菱形. 15.如图,空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是BC、CD上的点,且=,求证:直线EH与直线FG平行. 16.如图所示,在长方体ABCD-A1B1C1D1中的平面A1C1内有一点P,经过点P作棱BC的平行线,应该怎样画?并说明理由. 第8章 8.5 8.5.1直线与直线平行 一、选择题 1.B 由等角定理知,这两个三角形的三个角分别对应相等,所以这两个三角形相似. 2.D 如图所示,因为E,D,F分别为AB,PA,AC的中点,可得DE∥PB,EF∥BC, 又因为PB⊥BC,所以DE⊥EF,所以∠DEF=90°. 故选D. 3.D 分别与两条异面直线平行的直线不可能平行,否则,由基本性质4可得原来的两条异面直线平行,与两直线异面矛盾.但可以相交或异面. 4.C 由题意结合三角形中位线的性质,可得FH∥PA,GJ∥PA,由平行公理可得FH∥GJ. 5.A ∵E,F为中点,∴EF∥PN, 同理,HG∥PN,∴EF与HG平行. 6.C 如图,连接AD1,CD1,AC,则E,F分别为AD1,CD1的中点.由三角形的中位线定理,知EF∥AC,GH∥AC,所以EF∥GH,故选C. 7.ABD 根据过平面内一点和平面外一点的直线,与平面内不过该点的直线异面,可判定A,B中EF,MN异面;C中直线EF与MN有可能平行;D中,若EF∥MN,则过EF的平面与底面相交,EF就跟交线平行,则过点N有两条直线与EF平行,不可能.故选ABD. 8.ABC 由中位线定理,易知MQ∥BD,ME∥BC,QE∥CD,NP∥BD.有MQ∥NP,所以M,N,P,Q四点共面,故A说法正确 ... ...
~~ 您好,已阅读到文档的结尾了 ~~