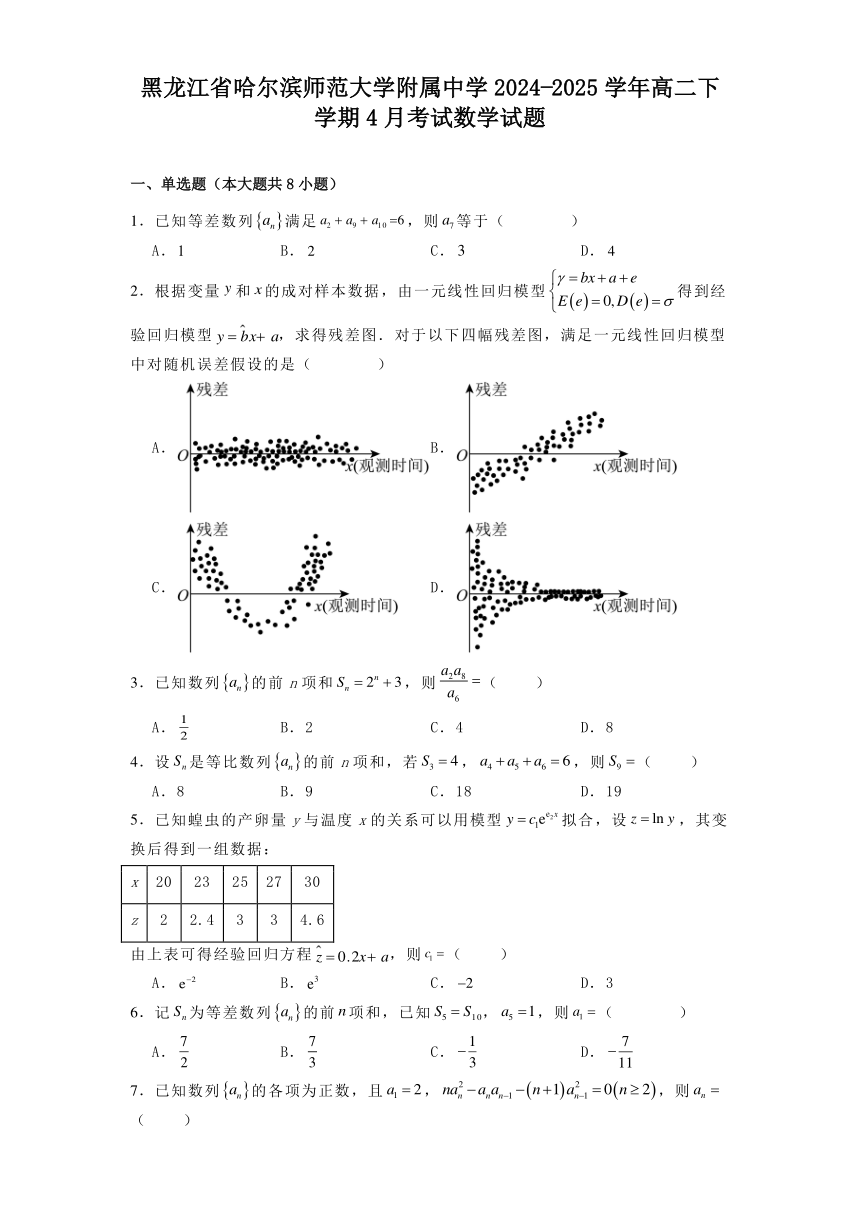
黑龙江省哈尔滨师范大学附属中学2024-2025学年高二下学期4月考试数学试题(含详解)

黑龙江省哈尔滨师范大学附属中学2024 2025学年高二下学期4月考试数学试题 一、单选题（本大题共8小题） 1．已知等差数列满足，则等于（ ） A． B． C． D． 2．根据变量和的成对样本数据，由一元线性回归模型得到经验回归模型，求得残差图．对于以下四幅残差图，满足一元线性回归模型中对随机误差假设的是（ ） A． B． C． D． 3．已知数列的前n项和，则（ ） A． B．2 C．4 D．8 4．设是等比数列的前n项和，若，，则（ ） A．8 B．9 C．18 D．19 5．已知蝗虫的产卵量y与温度x的关系可以用模型拟合，设，其变换后得到一组数据： x 20 23 25 27 30 z 2 2.4 3 3 4.6 由上表可得经验回归方程，则（ ） A． B． C． D．3 6．记为等差数列的前项和，已知，，则（ ） A． B． C． D． 7．已知数列的各项为正数，且，，则（ ） A． B． C． D． 8．若等差数列满足，则（ ） A．2025 B． C． D． 二、多选题（本大题共3小题） 9．下列的叙述正确的有（ ） A．关于一元线性回归，若相关系数，则y与x的相关程度很强 B．关于一元线性回归，若决定系数越大，模型的拟合效果越差 C．关于独立性检验，随机变量的值越大，认为“两个分类变量有关系”的把握性越大 D．关于独立性检验，若的观测值满足，依据小概率值的独立性检验，认为“两个分类变量无关”（参考数据：） 10．已知数列的前项和，则下列说法正确的是（ ） A． B．为中的最大项 C． D． 11．如图，有一列曲线，，……，，……，且1是边长为1的等边三角形，是对进行如下操作而得到：将曲线的每条边进行三等分，以每边中间部分的线段为边，向外作等边三角形，再将中间部分的线段去掉得到，记曲线的边数为，周长为，围成的面积为，则下列说法正确的是（ ） A．数列{}是首项为3，公比为4的等比数列 B．数列{}是首项为3，公比为的等比数列 C．数列是首项为，公比为的等比数列 D．当n无限增大时，趋近于定值 三、填空题（本大题共3小题） 12．已知数列中，，，，则 . 13．已知等差数列，的前n项和分别为，，且，则使得为整数的正整数n的值为 . 14．已知数列的前n项和，且，数列，均为等差数列，又数列的前n项和为，且，则的值为 . 四、解答题（本大题共5小题） 15．已知数列，，其中是各项均为正数的等比数列，满足，. (1)求数列的通项公式； (2)且，求数列的前2n项和. 16．已知数列满足（，），且. (1)求，，并证明数列是等比数列； (2)若，求数列的前n项和. 17．推进垃圾分类处理，是落实绿色发展理念的必然选择.为加强社区居民的垃圾分类意识，某社区在健身广场举办了“垃圾分类，从我做起”生活垃圾分类大型宣传活动，号召社区居民用实际行动为建设绿色家园贡献一份力量，为此需要征集一部分垃圾分类志愿者. (1)为调查社区居民喜欢担任垃圾分类志愿者是否与性别有关，现随机选取了一部分社区居民进行调查，其中被调查的男性居民30人，女性居民20人，男性居民中不喜欢担任垃圾分类志愿者占男性居民的，女性居民中不喜欢担任垃圾分类志愿者占女性居民的.根据所给数据，得到成对样本数据的分类统计结果，完成下面列联表，并依据小概率值的独立性检验，能否认为居民喜欢担任垃圾分类志愿者与性别有关？ 性别 合计 男性 女性 喜欢担任 不喜欢担任 合计 附：， 0.100 0.050 0.010 0.005 0.001 2.706 3.841 6.635 7.879 10.828 (2)若某垃圾站的日垃圾分拣量y（千克）与垃圾分类志愿者人数x（人）之间具有较强的线性相关性，求回归直线方程，并预测志愿者人数为10人时，该垃圾站的日垃圾分拣量. 数据统计如表： 志愿者人数x（人） 2 3 4 5 6 日垃圾分拣量y（千克） 24 29 41 46 60 参考数据，附：， 18．已知数列的前n项和为，且. (1)求数列的通项公式； (2)数列满足：，求数列的通项公式 ... ...