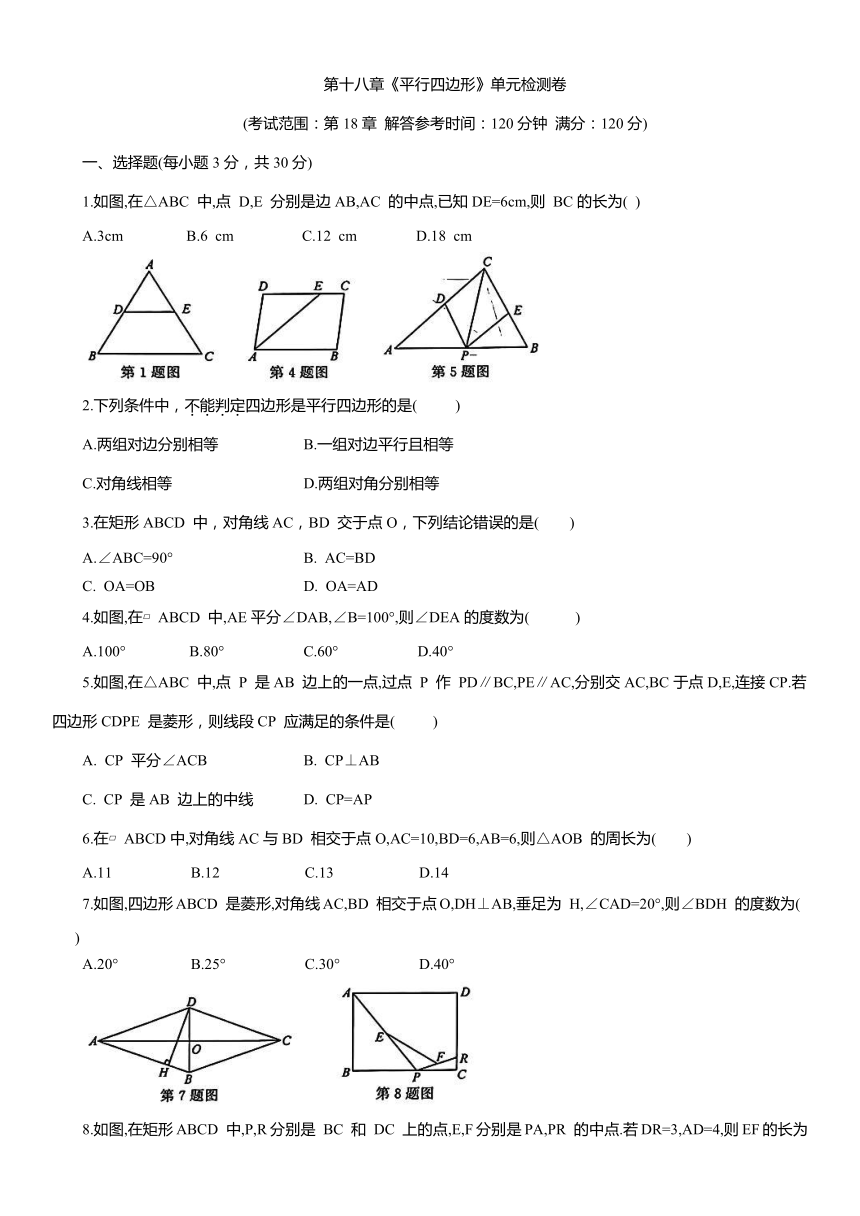
第十八章《平行四边形》单元检测卷（含答案）2024-2025学年人教版八年级数学下册

第十八章《平行四边形》单元检测卷 (考试范围：第18章 解答参考时间：120分钟 满分：120分) 一、选择题(每小题3分，共30分) 1.如图,在△ABC 中,点 D,E 分别是边AB,AC 的中点,已知DE=6cm,则 BC的长为( ) A.3cm B.6 cm C.12 cm D.18 cm 2.下列条件中，不能判定四边形是平行四边形的是( ) A.两组对边分别相等 B.一组对边平行且相等 C.对角线相等 D.两组对角分别相等 3.在矩形ABCD 中，对角线AC，BD 交于点O，下列结论错误的是( ) A.∠ABC=90° B. AC=BD C. OA=OB D. OA=AD 4.如图,在 ABCD 中,AE平分∠DAB,∠B=100°,则∠DEA的度数为( ) A.100° B.80° C.60° D.40° 5.如图,在△ABC 中,点 P 是AB 边上的一点,过点 P 作 PD∥BC,PE∥AC,分别交AC,BC于点D,E,连接CP.若四边形CDPE 是菱形，则线段CP 应满足的条件是( ) A. CP 平分∠ACB B. CP⊥AB C. CP 是AB 边上的中线 D. CP=AP 6.在 ABCD中,对角线AC与BD 相交于点O,AC=10,BD=6,AB=6,则△AOB 的周长为( ) A.11 B.12 C.13 D.14 7.如图,四边形ABCD 是菱形,对角线AC,BD 相交于点O,DH⊥AB,垂足为 H,∠CAD=20°,则∠BDH 的度数为( ) A.20° B.25° C.30° D.40° 8.如图,在矩形ABCD 中,P,R分别是 BC 和 DC 上的点,E,F分别是PA,PR 的中点.若DR=3,AD=4,则EF的长为( ) A.2.5 B.3 C.4 D.5 9.如图,在△ABC 中, 点 D 在 BC 的延长线上，且 若∠D=40°,则∠B 的度数为( ) A.10° B.20° C.30° 10.如图,正方形ABCD 的边长为6,点 E,F 分别在AB,AD 上,若 且∠ECF=45°,则AF 的长为( ) A.4 B.3 C.2.5 D.2 二、填空题(每小题3分，共15分) 11.如图,E,F 是 ABCD 的对角线BD 上的两点,请你添加一个适当的条件: ,使AE⊥CF. 12.已知菱形的面积是12cm ，它的一条对角线长为6cm，则另一条对角线长为 cm. 13.如图,矩形ABCD 的对角线AC 和BD 相交于点O,过点O的直线分别交 AD 和BC 于点E,F,AB=2,BC=3,则图中阴影部分的面积为 . 14.如图,在矩形 ABCD 中,点 E 是BC 上的一点,DF⊥AE,垂足为点 F.若AB=3,AE=AD=5,则AF 的长为 15.如图,在 ABCD 中,点O是对角线AC 的中点,点 E 在边AB 上,连接DE,取DE 的中点F,连接EO并延长,交CD 于点G.若DG=3CG,OF=2,则AE 的长为 . 三、解答题(共9小题，共75分) 16.(本题6分)如图,在 中， 垂足E在CA 的延长线上， 垂足F在AC 的延长线上，求证： 17.(本题6分)如图,在 中，E，F 是对角线BD 上的两点，且 求证：四边形AECF 是平行四边形. 18.(本题6分)如图,在 中， CD 为AB 边上的高，CE 为AB 边上的中线， ,求CD 的长. 19.(本题8分)某人买了一盏简单而精致的吊灯(图1)，其正面的平面图如图2所示，四边形ABCD 是一个菱形外框架，对角线AC,BD 相交于点O,四边形 AECF 是其内部框架,点 E,F在BD 上,且 (1)求证:四边形AECF 为菱形. (2)若 AE⊥AD,F 为 DE 的中点, ，求四边形AECF 的周长. 20.(本题8分)如图,在 中，以点A 为圆心，AB 的长为半径画弧交AD 于点F，再分别以点B，F为圆心，大于 的长为半径画弧，两弧交于点 P，直线 AP 交BC 于点E.，连接EF. (1)请用尺规作图法画出图形，并保留作图痕迹； (2)若 判断四边形 ABEF 的形状，并求其面积… 21.(本题8分)如图,E,F,G分别是五边形ABCHD 的边AD,AB,BC的中点, 且 连接DB. (1)试探究 DH 与BD 应满足什么条件时，总有 (2)直接写出DH 与BD 满足 时, 22.(本题10分)如图,四边形 ABCD 为正方形,E 为对角线AC上一动点，连接 DE，过点 E 作. 交 BC 于点 F,以DE,EF 为邻边作矩形DEFG,连接CG. (1)求证:矩形 DEFG 是正方形; (2)猜想CE与CG 之间的位置关系，并说明理由. 23.(本题11分)定义：两边的平方和等于第三边平方的3倍的三角形叫做非凡三角形.例如：某三角形三边长分别是 2 和3，因为 所以这个三角形是非凡三角形. (1)若 是非凡三角形，且 则 ; (2) ... ...