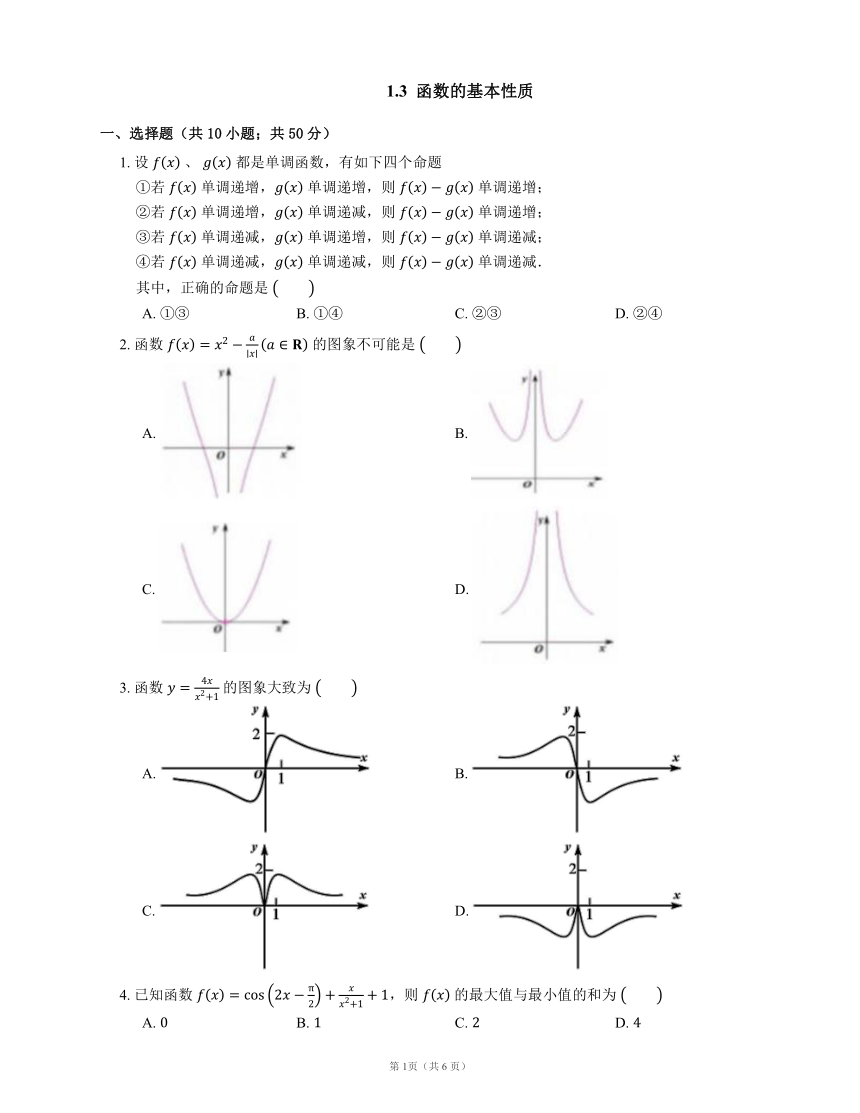
1.3 函数的基本性质 一、选择题(共10小题;共50分) 1. 设 、 都是单调函数,有如下四个命题 ①若 单调递增, 单调递增,则 单调递增; ②若 单调递增, 单调递减,则 单调递增; ③若 单调递减, 单调递增,则 单调递减; ④若 单调递减, 单调递减,则 单调递减. 其中,正确的命题是 A. ①③ B. ①④ C. ②③ D. ②④ 2. 函数 的图象不可能是 A. B. C. D. 3. 函数 的图象大致为 A. B. C. D. 4. 已知函数 ,则 的最大值与最小值的和为 A. B. C. D. 5. 函数 和 的递增区间依次是 A. , B. , C. , D. , 6. 已知函数 在 上的最大值为 则 的取值范围是 A. B. C. D. 7. 已知 ,且 ,则 A. B. C. D. 8. 已知 是定义在 上的偶函数,且 在 内单调递减,则 A. B. C. D. 9. 已知函数 在区间 上的最大值是 ,那么实数 的取值范围是 A. B. C. D. 10. 已知 是定义在 上的偶函数,且在区间 上单调递增,设 ,,,则 A. B. C. D. 二、填空题(共5小题;共25分) 11. 函数 在区间 上的最大值为 ,则 . 12. 已知 是定义在 上的奇函数,当 时, 的图象如右图所示,那么 的值域是 . 13. 函数 的单调递增区间是 . 14. 已知函数 的最小值为 ,则实数 . 15. , 都是定义在 上的奇函数,且 .若 ,则 . 三、解答题(共3小题;共39分) 16. 已知:函数 . (1)当 为何值时, 为偶函数 (2)当 为何值时, 为奇函数 17. (1)已知 ,求函数 的最小值; (2)已知 ,求函数 的最小值. 18. 试判断函数 在 上的单调性,并加以证明. 答案 第一部分 1. C 【解析】 当 是单调增函数时, 是单调减函数, 是单调减函数时, 是单调增函数, 根据两个单调增函数相加是增函数,两个单调减函数相加是减函数这一原理,易知 ② ③ 正确. 2. D 【解析】当 时函数 图象可能为A; 当 时函数 图象可能为B; 当 时函数 图象可能为C. 3. A 【解析】由函数的解析式可得:, 则函数 为奇函数,其图象关于坐标原点对称,选项C,D错误; 当 时,,选项B错误. 4. C 【解析】函数 设函数 ,, 则 所以 是 上的奇函数, 设 的最大值为 ,则 的最小值为 , 所以 的最大值为 ,最小值为 , 所以 , 即 的最大值与最小值的和为 . 故选C. 5. C 【解析】因为 的递增区间为 , 又 的递增区间为 . 6. D 【解析】 的图象如下图所示, 对称轴为 ,,令 ,得 ,因为 ,所以数形结合可得 或 . 7. A 【解析】令 ,易知 是 上的奇函数, 所以 , 又 , 所以 , 所以 , 所以 , 所以 . 8. C 【解析】根据题意, 是定义在 上的偶函数, 则 , 又由 在 内单调递减,且 , 则有 , 即有 . 9. B 10. C 【解析】根据题意, 是偶函数,且在区间 上单调递增,则 在 上单调递减, 则 ,,, 又由 , 则 . 第二部分 11. 【解析】若 ,则函数 在区间 上单调递减,并且在区间的左端点处取得最大值,即 ,解得 ,不满足 ,舍去;若 ,则函数 在区间 上单调递增,并且在区间的右端点处取得最大值,即 ,解得 .综上,. 12. 13. 【解析】本题考查函数的单调性.因为由 得函数 的定义域为 ,且函数 在 内为增函数,所以函数 的单调递增区间为 . 14. 15. 【解析】因为函数 , 均为奇函数, 所以 ,, 所以 , 所以 . 第三部分 16. (1) ,, 若 是偶函数,则可得 , 此时 ,是偶函数. (2) ,若 是奇函数,则 ,可得 , 此时 ,是奇函数. 17. (1) 因为 ,所以 . (当且仅当 ),即 时取" ". 所以函数 的最小值为 . (2) 因为 ,所以 (当且仅当 ,即 时取" "). 所以函数 的最小值为 . 18. 方法一:设 ,, 因为 , 所以 ,, 所以 ,即 , 故 在 上单调递增. 方法二:, 当 时,, 故 在 上为增函数. 第1页(共1 页) ... ...
~~ 您好,已阅读到文档的结尾了 ~~