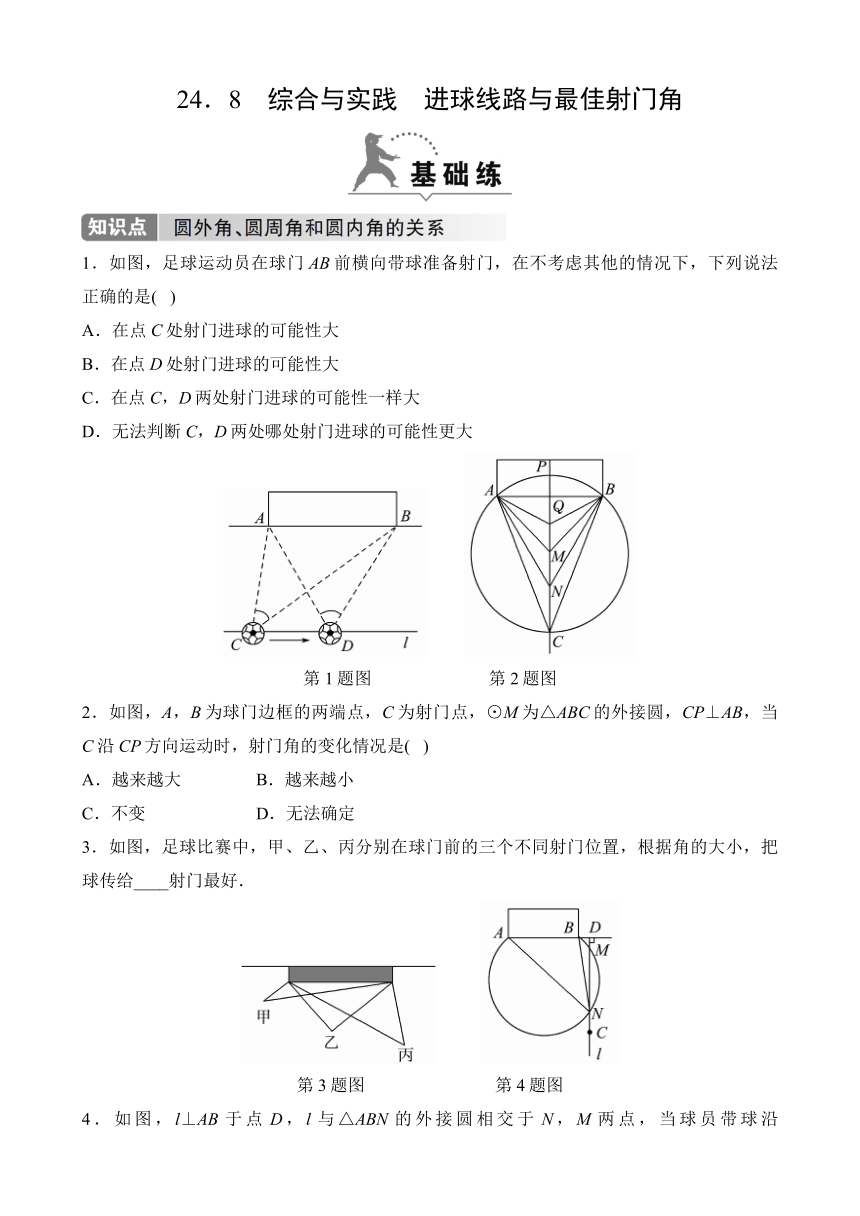
24.8 综合与实践 进球线路与最佳射门角 同步练习（含答案）

24．8　综合与实践　进球线路与最佳射门角 1．如图，足球运动员在球门AB前横向带球准备射门，在不考虑其他的情况下，下列说法正确的是( ) A．在点C处射门进球的可能性大 B．在点D处射门进球的可能性大 C．在点C，D两处射门进球的可能性一样大 D．无法判断C，D两处哪处射门进球的可能性更大 第1题图 　　　第2题图 2．如图，A，B为球门边框的两端点，C为射门点，⊙M为△ABC的外接圆，CP⊥AB，当C沿CP方向运动时，射门角的变化情况是( ) A．越来越大 B．越来越小 C．不变 D．无法确定 3．如图，足球比赛中，甲、乙、丙分别在球门前的三个不同射门位置，根据角的大小，把球传给____射门最好． 第3题图 　　　第4题图 4．如图，l⊥AB于点D，l与△ABN的外接圆相交于N，M两点，当球员带球沿C→N→M→D运动时，射门角先逐渐变____，再逐渐变____． 5．足球训练场上教练在球门前画了一个圆圈进行无人防守的射门训练．如图，甲、乙两名运动员分别在点C，D两处，他们争论不休，都说自己所在的位置对球门AB的张角大，如果你是教练，请评一评他们两个人谁的位置对球门AB的张角大．为什么？ 6．平面内不在同一条直线上的三点确定一个圆，那么平面内的四点(任意三点均不在同一条直线上)，能否在同一个圆上呢？ 设不在同一条直线上的三点A，B，C确定的圆为⊙O，当C，D在线段AB的同侧时． (1)如图1所示，若点D在⊙O上，此时有∠ACB＝∠ADB，理由是_____； (2)如图2所示，若点D在⊙O内，此时有∠ACB__ __∠ADB；如图3所示，若点D在⊙O外，此时有∠ACB_ __∠ADB；(填“＝”“>”或“<”) (3)由上面的探究，请直接写出A，B，C，D四点在同一个圆上的条件：_____． 7．船在航行过程中，船长常常通过测定角度来确定是否会遇到暗礁． 如图所示，在小岛周围内有暗礁，在A，B两处建有两座航标灯塔，且∠APB＝θ，船要在两灯塔北侧绕过暗礁区，应怎样航行？为什么？ 24．8　综合与实践　进球线路与最佳射门角 1．如图，足球运动员在球门AB前横向带球准备射门，在不考虑其他的情况下，下列说法正确的是( B ) A．在点C处射门进球的可能性大 B．在点D处射门进球的可能性大 C．在点C，D两处射门进球的可能性一样大 D．无法判断C，D两处哪处射门进球的可能性更大 第1题图 　　　第2题图 2．如图，A，B为球门边框的两端点，C为射门点，⊙M为△ABC的外接圆，CP⊥AB，当C沿CP方向运动时，射门角的变化情况是( A ) A．越来越大 B．越来越小 C．不变 D．无法确定 3．如图，足球比赛中，甲、乙、丙分别在球门前的三个不同射门位置，根据角的大小，把球传给__乙__射门最好． 第3题图 　　　第4题图 4．如图，l⊥AB于点D，l与△ABN的外接圆相交于N，M两点，当球员带球沿C→N→M→D运动时，射门角先逐渐变__大__，再逐渐变__小__． 5．足球训练场上教练在球门前画了一个圆圈进行无人防守的射门训练．如图，甲、乙两名运动员分别在点C，D两处，他们争论不休，都说自己所在的位置对球门AB的张角大，如果你是教练，请评一评他们两个人谁的位置对球门AB的张角大．为什么？ 解：甲、乙两人所在的位置对球门AB的张角一样大．理由：根据圆周角定理的推论可得∠ADB＝∠ACB. 6．平面内不在同一条直线上的三点确定一个圆，那么平面内的四点(任意三点均不在同一条直线上)，能否在同一个圆上呢？ 设不在同一条直线上的三点A，B，C确定的圆为⊙O，当C，D在线段AB的同侧时． (1)如图1所示，若点D在⊙O上，此时有∠ACB＝∠ADB，理由是__同弧所对的圆周角相等__； (2)如图2所示，若点D在⊙O内，此时有∠ACB__<__∠ADB；如图3所示，若点D在⊙O外，此时有∠ACB__>__∠ADB；(填“＝”“>”或“<”) (3)由上面的探究，请直接写出A，B，C，D四点在同一个圆上的条件：__C，D在线段AB的同侧且∠ ... ...