3.4数据的离散程度(1) 导学案

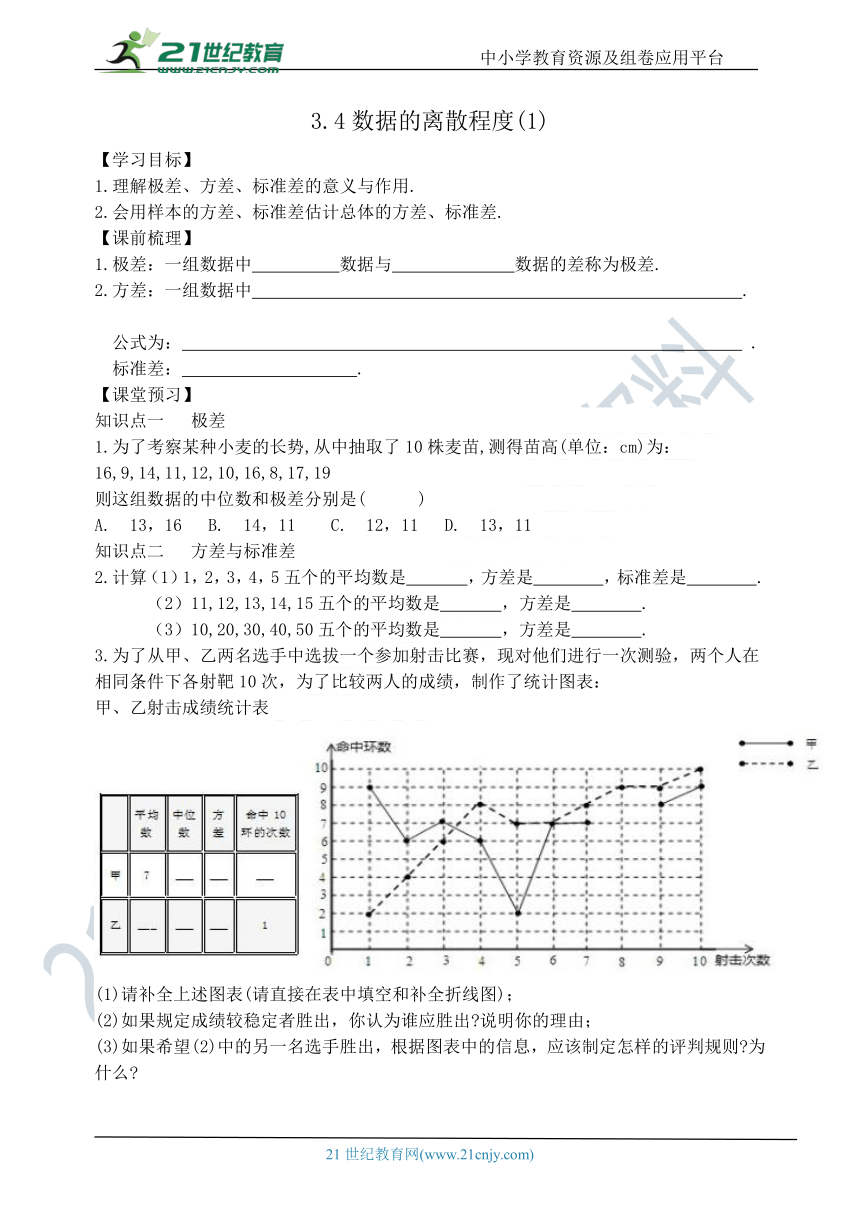
中小学教育资源及组卷应用平台 3.4数据的离散程度(1) 【学习目标】 1.理解极差、方差、标准差的意义与作用. 2.会用样本的方差、标准差估计总体的方差、标准差. 【课前梳理】 1.极差：一组数据中 数据与 数据的差称为极差. 2.方差：一组数据中 . 公式为： . 标准差： . 【课堂预习】 知识点一 极差 1.为了考察某种小麦的长势,从中抽取了10株麦苗,测得苗高(单位：cm)为： 16,9,14,11,12,10,16,8,17,19 则这组数据的中位数和极差分别是( ) A. 13，16 B. 14，11 C. 12，11 D. 13，11 知识点二 方差与标准差 2.计算（1）1，2，3，4，5五个的平均数是 ，方差是 ，标准差是 . （2）11,12,13,14,15五个的平均数是 ，方差是 . （3）10,20,30,40,50五个的平均数是 ，方差是 . 3.为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了统计图表： 甲、乙射击成绩统计表 (1)请补全上述图表(请直接在表中填空和补全折线图)； (2)如果规定成绩较稳定者胜出，你认为谁应胜出 说明你的理由； (3)如果希望(2)中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则 为什么 【当堂达标】 1.如果样本方差，那么这个样本的平均数为 ，样本容量为 . 2.从甲、乙、丙、丁四人中选一人参加诗词大会比赛，经过三轮初赛，他们的平均成绩都是86.5分，方差分别是S甲2=1.5，S乙2=2.6，S丙2=3.5，S丁2=3.68，你认为派谁去参赛更合适（　　） A.甲 B.乙 C.丙 D.丁 3.一组数据：，，0，，1的平均数是0，则= ,= . 4.已知一组数据0，1，2，3，4的方差为2，则数据20,21,22,23,24的方差为_____. 5.某班第二组女生参加体育测试，仰卧起坐的成绩（单位：个）如下：43，41，39，40，37.这组数据方差是　 　.标准差是　 　. 【课后巩固】 1.为参加学校举办的“诗意校园 致远方”朗诵艺术大赛，八年级“屈原读书社”组织了五次选拔赛，这五次选拔赛中，小明五次成绩的平均数是90，方差是2；小强五次成绩的平均数也是90，方差是14.8.下列说法正确的是（　　） A.小明的成绩比小强稳定 B.小明、小强两人成绩一样稳定 C.小强的成绩比小明稳定 D.无法确定小明、小强的成绩谁更稳定 2.贵州省第十届运动会将于2018年8月8日在遵义市奥体中心开幕，某校有2名射击队员在比赛中的平均成绩均为9环，如果教练要从中选1名成绩稳定的队员参加比赛，那么还应考虑这2名队员选拔成绩的（　　） A.方差 B.中位数 C.众数 D.最高环数 3.王大伯几年前承包了甲、乙两片荒山，各栽100棵杨梅树，成活98%.现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的杨梅，每棵的产量如折线统计图所示. (1)分别计算甲、乙两山样本的平均数，并估算出甲、乙两山杨梅的产量总和； (2)试通过计算说明，哪个山上的杨梅产量较稳定 3.4数据的离散程度(1) 【课堂预习】 1. D 2.（1）3，2， （2）13，2 （3）30，200 3.（1） （2）由甲的方差小于乙的方差，甲比较稳定，故甲胜出； （3）如果希望乙胜出，应该制定的评判规则为：平均成绩高的胜出；如果平均成绩相同，则随着比赛的进行，发挥越来越好者或命中满环（10环）次数多者胜出．因为甲乙的平均成绩相同，乙只有第5次射击比第四次射击少命中1环，且命中1次10环，而甲第2次比第1次、第4次比第3次，第5次比第4次命中环数都低，且命中10环的次数为0次，即随着比赛的进行，有可能乙的射击成绩越来越好． 【当堂达标】 1.2,4 2.A 3.2，2 4.2 5.4，2 【课后巩固】 1.A 2.A 3.解：(1)x 甲=40(千克),(1分)x 乙=40(千克)， 总产量为40×100×98%×2=7840(千克)； (2)S2甲=1/4[(50 40)2+(36 40)2+(40 40)2+(34 40)2]=38(千克2)， S2乙=1/4[(36 40)2+(4 ... ...