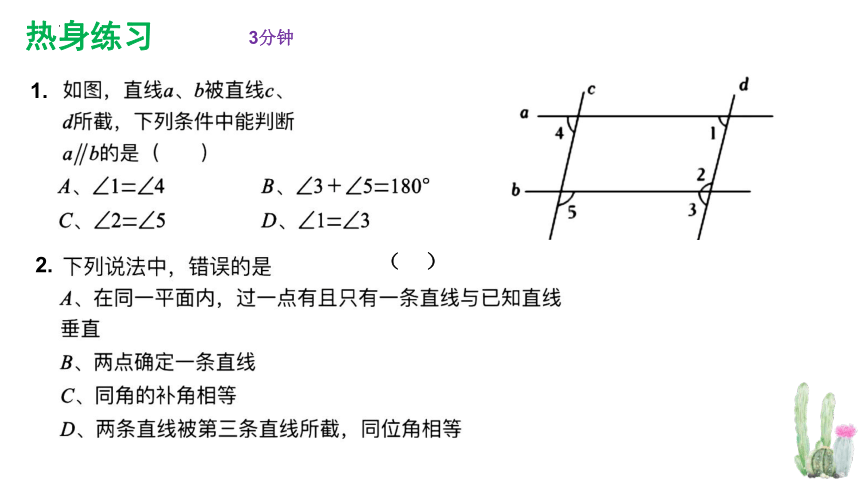
热身练习 1. 2. 3分钟 ( ) 7.2探索直线平行的条件(练习) 学习目标 1.能结合图形识别同位角、内错角、同旁内角,理解同位角、内错角、同旁内角的概念。 2. 会运用同位角、内错角、同旁内角判定两条直线平行,进一步发展合情推理能力。 2分钟 温故 1、观察右图并填空: ∠1 与 是同位角; (2) ∠5 与 是同旁内角; (3) ∠1 与 是内错角; 同位角、内错角、同旁内角的概念 一 同旁内角是 形状 内错角是 形状 F 1 3 7 5 2 8 6 D C A B E 4 ①位于两条被截直线同一方、 ② 位于两条被截直线的 , 且在截线的 的两个角,叫做内错角;∠7与∠2 且在截线同一侧的两个角,叫做 ; ∠1与∠2 同位角 内部 两侧 ③ 位于两条被截直线 , 且在截线的 的两个角, 叫做同旁内角 .∠5与∠2 内部 同旁 Z U “三线八角”小结 同位角是 F 形状 考考你的眼力 2 4 观察下面每幅图中的直线a,b,它们分别平行吗?你能验证吗? 复习回顾 填空: (1)∵ ∠1=∠2 (已知) ∴ ∥ ( ) (2)∵ ∠2= ___ ∴ ∥ ,(同位角相等,两直线平行) (3)∵ ∠3+∠4=180° ∴ ∥ ,( ) (4) AC与FG是否平行,请说明理由 1 2 3 4 A B C D E F G 内错角相等,两直线平行 同旁内角互补,两直线平行 F 1 3 7 5 2 8 6 D C A B E 4 三线八角 两直线平行的判定方法 ①定义:在同一平面内不相交的两条直线是平行线. ②平行于同一条直线的两条直线互相平行 ③同位角相等,两直线平行. ④内错角相等,两直线平行 ⑤同旁内角互补,两直线平行 知识梳理 例1.如图,一条街道的两个拐角∠ABC和∠BCD均为150°,街道AB与CD平行吗?为什么? 典型例题 1.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( ) A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50° C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50° 2.如图,一条公路修到湖边时,需要拐弯绕湖而过,第一次拐的角∠A=110°,第二次拐的角∠B=145°,则第三次拐的角∠C= 时,道路CE才能恰好与AD平行。 变式练习 例2.如图, AB⊥BC于点B,BC⊥CD于点C,∠1=∠2,那么EB∥CF吗?为什么? 挑战自我 例3.如图,已知PE平分∠BEF,PF平分∠DFE,∠1=35°,∠2=55° . (1)试说明: AB//CD ; (2)求 ∠AEP+∠CFP+∠EPF 的度数 ? 10分钟 当堂达标 1.下列图形中,由∠1=∠2能得到AB∥CD 的是( ) 2. 在平面内,下列四个说法中,正确的是( ) A.经过一点有且只有一条线段与已知直线垂直 B.经过一点有且只有一条线段与已知直线平行 C.经过一点有且只有一条直线与已知直线垂直 D.经过一点有且只有一条直线与已知直线平行 3.如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由. 3. 已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE. 4.已知:如图,∠DCE=∠E,∠B=∠D.求证:AD∥BC. 课堂小结 同位角、内错角、同旁内角的结构特征: 两条直线被第三条直线所截 同位角 “F”型 内错角 “Z”型 同旁内角 “U”型 课堂小结 ... ...
~~ 您好,已阅读到文档的结尾了 ~~