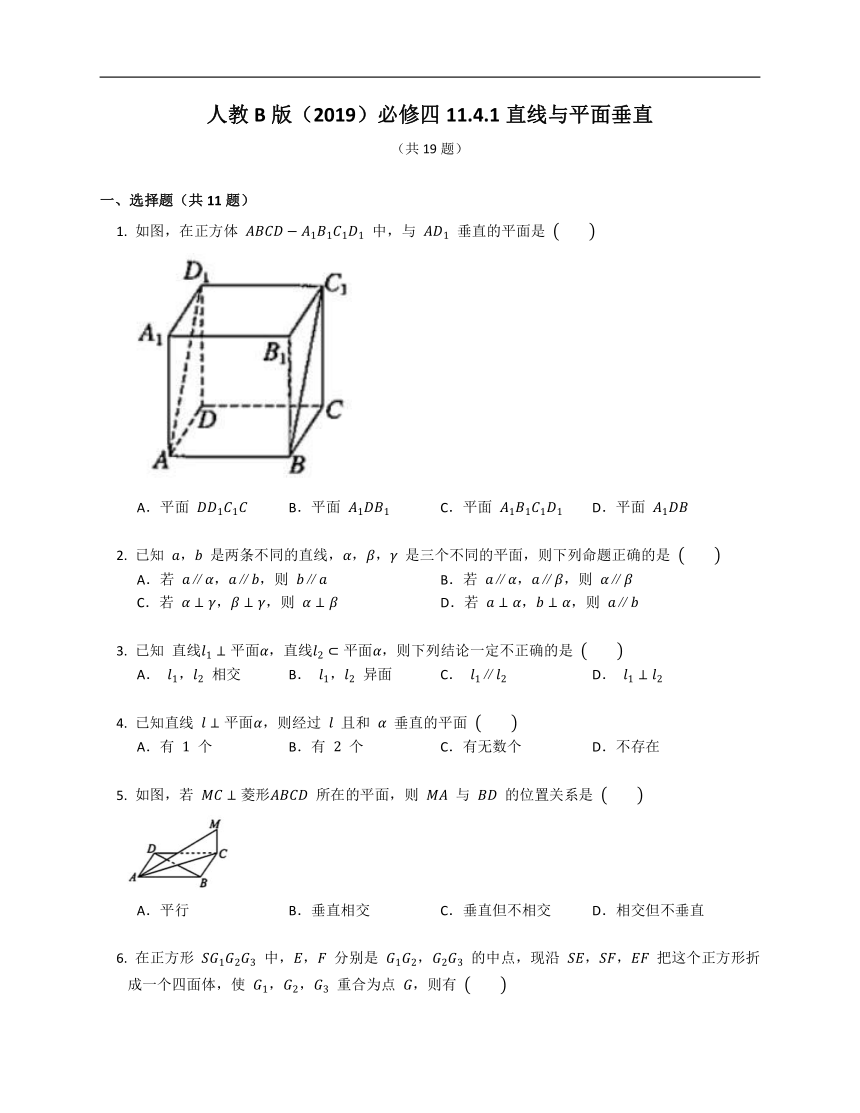
人教B版(2019)必修四11.4.1直线与平面垂直 (共19题) 一、选择题(共11题) 如图,在正方体 中,与 垂直的平面是 A.平面 B.平面 C.平面 D.平面 已知 , 是两条不同的直线,,, 是三个不同的平面,则下列命题正确的是 A.若 ,,则 B.若 ,,则 C.若 ,,则 D.若 ,,则 已知 ,,则下列结论一定不正确的是 A. , 相交 B. , 异面 C. D. 已知直线 ,则经过 且和 垂直的平面 A.有 个 B.有 个 C.有无数个 D.不存在 如图,若 所在的平面,则 与 的位置关系是 A.平行 B.垂直相交 C.垂直但不相交 D.相交但不垂直 在正方形 中,, 分别是 , 的中点,现沿 ,, 把这个正方形折成一个四面体,使 ,, 重合为点 ,则有 A. B. C. D. 如图,在正方形 中,, 分别为 , 的中点, 是 的中点.现沿 ,, 把这个正方形折成一个几何体,使 ,, 三点重合于点 ,则下列结论中成立的是 A. B. C. D. 如图,已知线段 垂直于定圆所在的平面,, 是 上的两个点, 是点 在 上的射影,当点 运动时,点 运动的轨迹是 A.圆 B.椭圆 C.抛物线 D.不是平面图形 如图,三棱锥 中,已知 , 于 ,,设 ,,记函数 ,则下列表述正确的是 A. 是关于 的增函数 B. 是关于 的减函数 C. 关于 先递增后递减 D. 关于 先递减后递增 如图,若 是长方体 被平面 截去几何体 后得到的几何体,其中 为线段 上异于 的点, 为线段 上异于 的点,且 ,则下列结论中不正确的是 A. B.四边形 是矩形 C. 是棱柱 D. 是棱台 如图,正方体 的棱长为 ,线段 上有两个动点 ,,且 .给出下列四个结论: ① ; ② 三棱锥 的体积为定值; ③ 在底面 内的正投影是面积为定值的三角形 ④ 在平面 内存在无数条与平面 平行的直线 其中,正确结论的个数是 A. B. C. D. 二、填空题(共4题) 在四棱锥 中,底面 为正方形, 底面 ,,,, 分别是棱 ,, 的中点,对于平面 截四棱锥 所得的截面多边形,有以下三个结论: ①截面的面积等于 ; ②截面是一个五边形; ③截面只与四棱锥 四条侧棱中的三条相交. 其中,所有正确结论的序号是 . 已知三棱锥 的三条侧棱都相等,顶点 在底面 上的射影为 ,则 是 的 心. 如图,在四面体 中,若截面 是正方形,则在下列命题中,正确的是 . ① ; ② ; ③ ; ④ . 如图,在 中,,,,,, 是 上的一个动点,则 的最小值为 . 三、解答题(共4题) 如图,在三棱锥 中,, 是 的中点,且 . (1) 求证:; (2) 若 ,求证:. 如图,在四棱锥 中,底面 是矩形,,, 是 的中点,, 分别在 , 上,且 ,.证明:. 如图 ,在等腰梯形ABCD中,,,,, 、 分别为腰 、 的中点.将四边形 沿 折起,使平面 ,如图 ,, 分别为线段 、 的中点. (1) 求证:; (2) 请在图 所给的点中找出两个点,使得这两点所在直线与平面 垂直,并给出证明; (3) 若 为线段 中点,在直线 上是否存在点 ,使得 面 ?如果存在,求出线段 的长度,如果不存在,请说明理由. 如图,四棱锥 中,底面 为菱形,. (1) 求证:. (2) 若 ,,,求三棱锥 的体积. 答案 一、选择题(共11题) 1. 【答案】B 【解析】因为 ,,,, 所以 . 2. 【答案】D 【解析】由 , 是两条不同的直线,,, 是三个不同的平面,知: 在A中,若 ,,则 或 ,故A错误; 在B中,若 ,,则 与 相交或平行,故B错误; 在C中,若 ,,则 与 相交或平行,故C错误; 在D中,若 ,,则由线面垂直的性质定理得 ,故D正确. 故选:D. 3. 【答案】C 【解析】由平面的垂线的定义可知,在平面 内肯定不存在与直线 平行的直线. 4. 【答案】C 【解析】经过 的平面都与 垂直,而经过 的平面有无数个. 5. 【答案】C 【解析】因为四边形 是菱形, 所以 . 因为 , 所以 因为 , ... ...
~~ 您好,已阅读到文档的结尾了 ~~