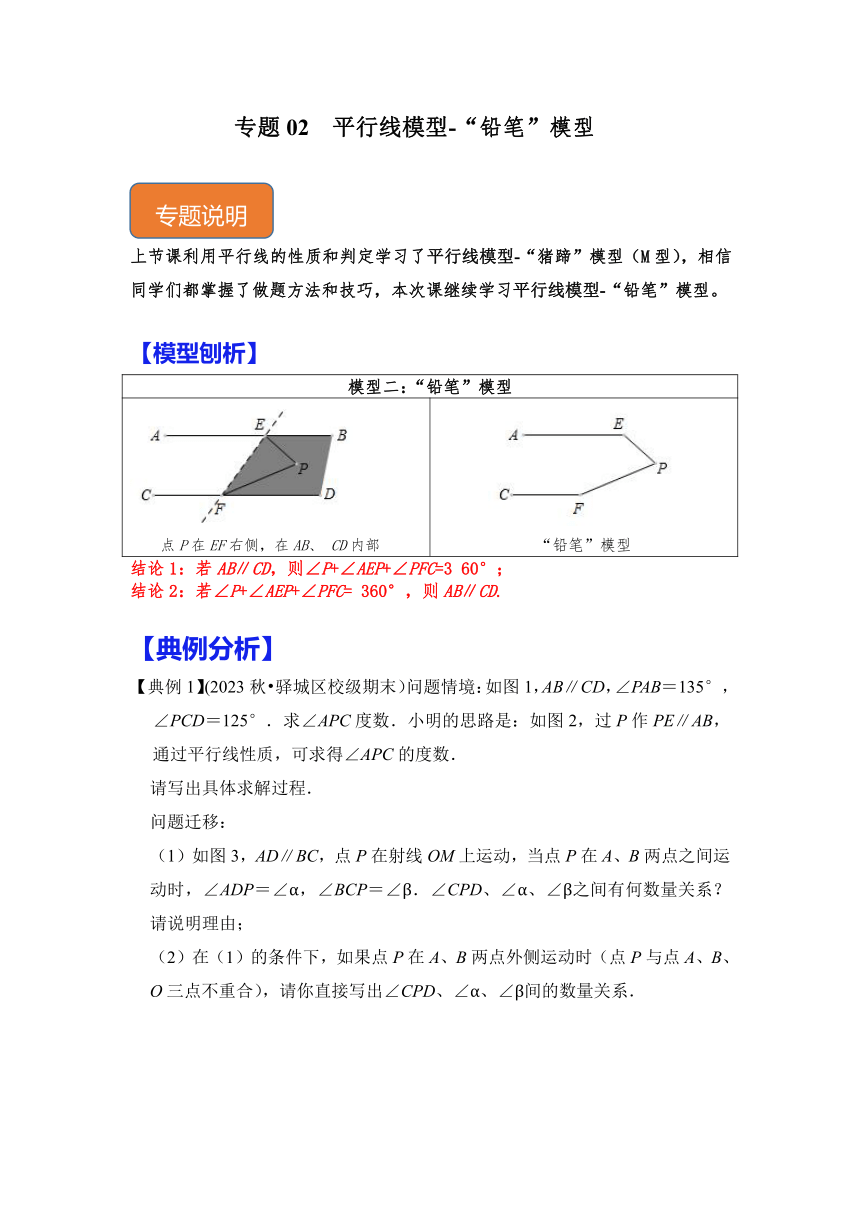
专题02 平行线模型-“铅笔”模型 上节课利用平行线的性质和判定学行线模型-“猪蹄”模型(M型),相信同学们都掌握了做题方法和技巧,本次课继续学习平行线模型-“铅笔”模型。 【模型刨析】 模型二:“铅笔”模型 点P在EF右侧,在AB、 CD内部 “铅笔”模型 结论1:若AB∥CD,则∠P+∠AEP+∠PFC=3 60°; 结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD. 【典例分析】 【典例1】(2023秋 驿城区校级期末)问题情境:如图1,AB∥CD,∠PAB=135°,∠PCD=125°.求∠APC度数.小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可求得∠APC的度数. 请写出具体求解过程. 问题迁移: (1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由; (2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系. 【变式1-1】(2023春 常州期中)问题情境:如图①,直线AB∥CD,点E,F分别在直线AB,CD上. 猜想:(1)若∠1=130°,∠2=150°,试猜想∠P= °; 探究:(2)在图①中探究∠1,∠2,∠P之间的数量关系,并证明你的结论; 拓展:(3)将图①变为图②,若∠1+∠2=325°,∠EPG=75°,求∠PGF的度数. 【变式1-2】(2023春 鹿邑县月考)如图,已知AB∥CD,∠ABE与∠CDE的平分线相交于点F. (1)如图1,若∠E=70°,求∠BFD的度数; (2)如图2,若∠ABM=∠ABF,∠CDM=∠CDF,写出∠M和∠E之间的数量关系,并证明你的结论. 【变式1-3】(2023秋 南岗区校级月考)已知:如图,AB∥CD (1)如图1,求证:∠A+∠E+∠D=360°; (2)如图2,若AF平分∠EAB,DF平分∠EDC.探究∠AFD与∠AED的数量关系 (直接写出结论). (3)如图3,在(2)的条件下,过A作AH∥ED交DC于点H,AD平分∠EAH,∠DAG:∠FDC=1:2,AF延长线交CD于点G.求:∠BAH的度数. 【夯实基础】 1.(2023秋 朝阳区校级期末)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=135°,则∠ABC= 度. 2.(2023秋 雁塔区校级期末)如图,直线l1∥l2,若∠1=35°,则∠2+∠3= . 3.(2023春 大兴区期末)如图,已知AB∥CD,E为AB,CD之间一点,连接BE,DE. (1)猜想∠BED时,∠B,∠D的数量关系,并证明; (2)作∠ABE,∠CDE的角平分线BF,DF交于点F. ①依题意补全图形; ②直接用等式表示∠BFD与∠BED的数量关系. 4.(2023秋 九江期末)实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射的光线为n. (1)当m∥n时,若∠1=50°,则∠2= ,∠3= ; (2)当m∥n时,若∠1=x°(0<x<90),则∠3= ; (3)根据(1)(2)结果,反过来猜想:当两平面镜a,b的夹角∠3为多少度时,m∥n.请说明理由(可以在图中添加适当的角度标记进行说明) 5.(2023春 普兰店区期中)直线AB∥CD,点E在AB和CD之间任一点,射线EF经过点B. (1)如图1,若DE∥AC,∠CAB=130°,∠ABF=80°,求∠DEB的度数; (2)如图2,若∠CAB=a,∠CDE=2∠ACD,若∠BED=140°,求∠ABE的度数(用含α式子表示). (3)如图3,若∠ABE的角平分线与∠CDE的角平分线交于点Q,试找出∠E和∠Q的数量关系并说明理由. 6.(2023春 宾阳县期中)如图,AB∥CD,点E,F分别在直线AB,CD上,点O在直线AB,CD之间,∠EOF=100°. (1)如图1,求∠BEO+∠DFO的值: (2)如图2,当∠BEO的平分线与∠DFO的平分线交于点M时,求∠EMF的度数: (3)如图3 ... ...
~~ 您好,已阅读到文档的结尾了 ~~