2023-2024学年数学人教版七年级上册 课时提高练 4.1.1 课时3 立体图形的展开与折叠（含答案）

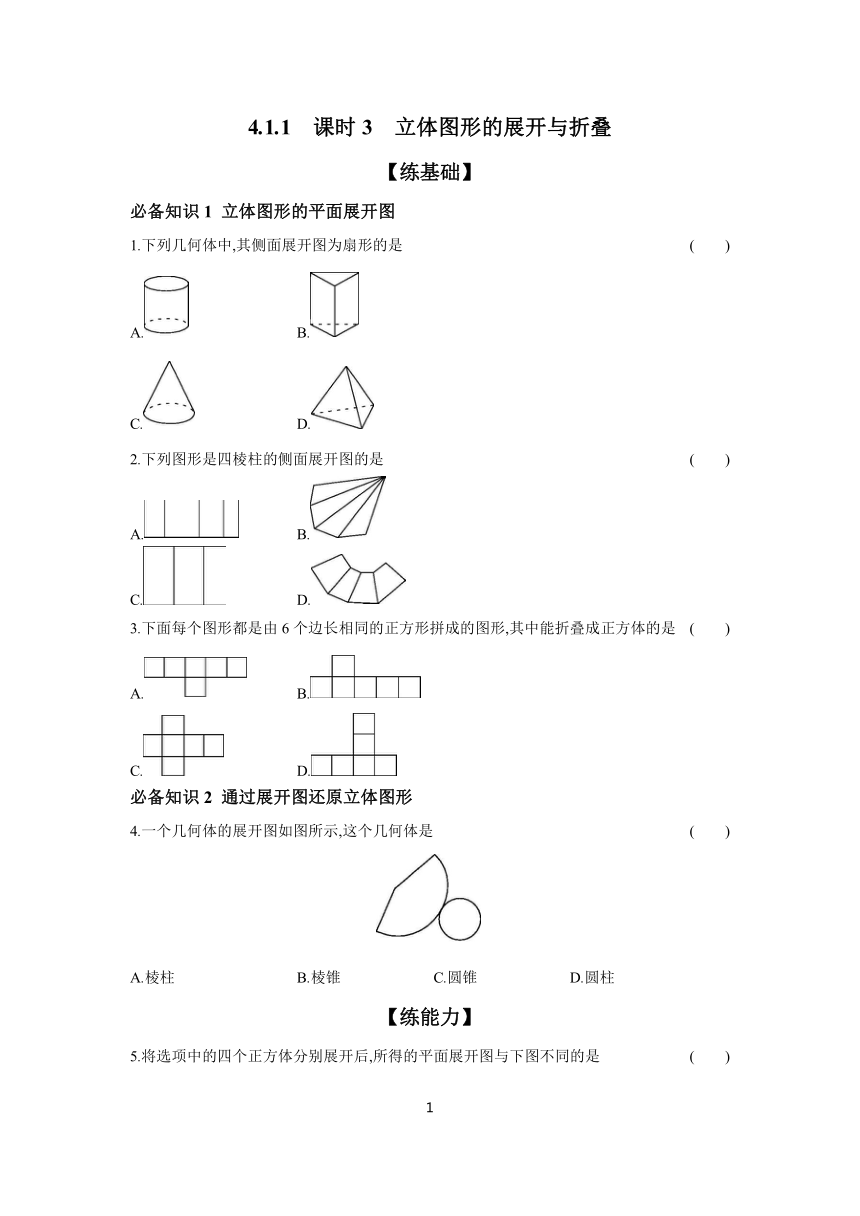
4.1.1　课时3　立体图形的展开与折叠 【练基础】 必备知识1 立体图形的平面展开图 1.下列几何体中,其侧面展开图为扇形的是 ( ) A. B. C.　 D. 2.下列图形是四棱柱的侧面展开图的是 ( ) A. B. C. D. 3.下面每个图形都是由6个边长相同的正方形拼成的图形,其中能折叠成正方体的是 ( ) A. B. C. D. 必备知识2 通过展开图还原立体图形 4.一个几何体的展开图如图所示,这个几何体是 ( ) A.棱柱 B.棱锥 C.圆锥 D.圆柱 【练能力】 5.将选项中的四个正方体分别展开后,所得的平面展开图与下图不同的是 ( ) A.　　　　　　　　　 B. C. D. 6.从如图所示的7个小正方形中剪去1个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去的小正方形上的字是 ( ) A.“美”或“中” B.“丽”或“中” C.“欢”或“您” D.“美”或“丽”或“迎” 7.【教材P123习题4.1T13变式】如图所示的正方体盒子展开后可以得到 ( ) A　　　 B　　　 C　 　　D 8.【教材P118练习T2变式】下列选项中,左边的图形能够折成右边的立体图形的是 ( ) A　　　　　　　B C　　　　　　　D 9.一个无盖的长方体盒子的展开图(重叠部分不计)如图所示,根据图中数据,则该无盖长方体盒子的体积为　 　cm3. 10.如图,这是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题: (1)如果A面在长方体的底部,那么哪一个面会在上面 (2)如果F面在前面,B面在右面,那么哪一个面会在上面 (字母朝外) 11.一个正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示. (1)A的对面是　 　,B的对面是　 　,C的对面是　 　.(直接用字母表示) (2)若A=1,B=-m-n,C=|m-1|,E=(1-n)2,且小正方体各对面上的两个数都互为相反数,请求出D所表示的数. 【练素养】 12.【问题情境】某综合实践小组进行废物再利用的环保小卫士行动.他们准备用废弃的宣传单制作装垃圾的无盖纸盒. 【操作探究】 (1)若准备制作一个无盖的正方体形纸盒,如图1,图形　 　经过折叠能围成无盖正方体形纸盒 (选择“A”、“B”、“C”或“D”) (2)如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字 (3)如图3,有一张边长为20 cm的正方形废弃宣传单,小华准备将其四个角各剪去一个小正方形,折成无盖长方体形纸盒. ①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕. ②若四个角各剪去了一个边长为4 cm的小正方形,问这个纸盒的底面积和容积分别为多少 参考答案 课时3　立体图形的展开与折叠 练基础 1.C　2.A　3.C　4.C 练能力 5.B　6.D　7.D　8.C 9.6000 10.【解析】由图可知,“A”与“C”相对,“B”与“E”相对,“D”与“F”相对, (1)因为面“A”与面“C”相对,所以A面是长方体的底部时,C面在上面. (2)由图可知,如果F面在前面,B面在右面,那么“C”面在下面,因为“C”与“A”相对,所以A面会在上面. 11.【解析】(1)F;D;E. (2)因为小正方体各对面上的两个数都互为相反数, 所以|m-1|+(1-n)2=0, 解得m=1,n=1, 所以B=-1-1=-2, 所以D表示的数为2. 练素养 12.【解析】(1)C. (2)由正方体表面展开图的“相间、Z端是对面”可知,“保”与“卫”是对面,故答案为卫. (3)①所画出的图形如图所示. ②当小正方形的边长为4 cm时,纸盒的底面积为(20-2×4)2=122=144(cm2),纸盒的容积为4×(20-2×4)2=576(cm3). 答:纸盒的底面积为144 cm2,纸盒的容积为576 cm3. 2 ... ...