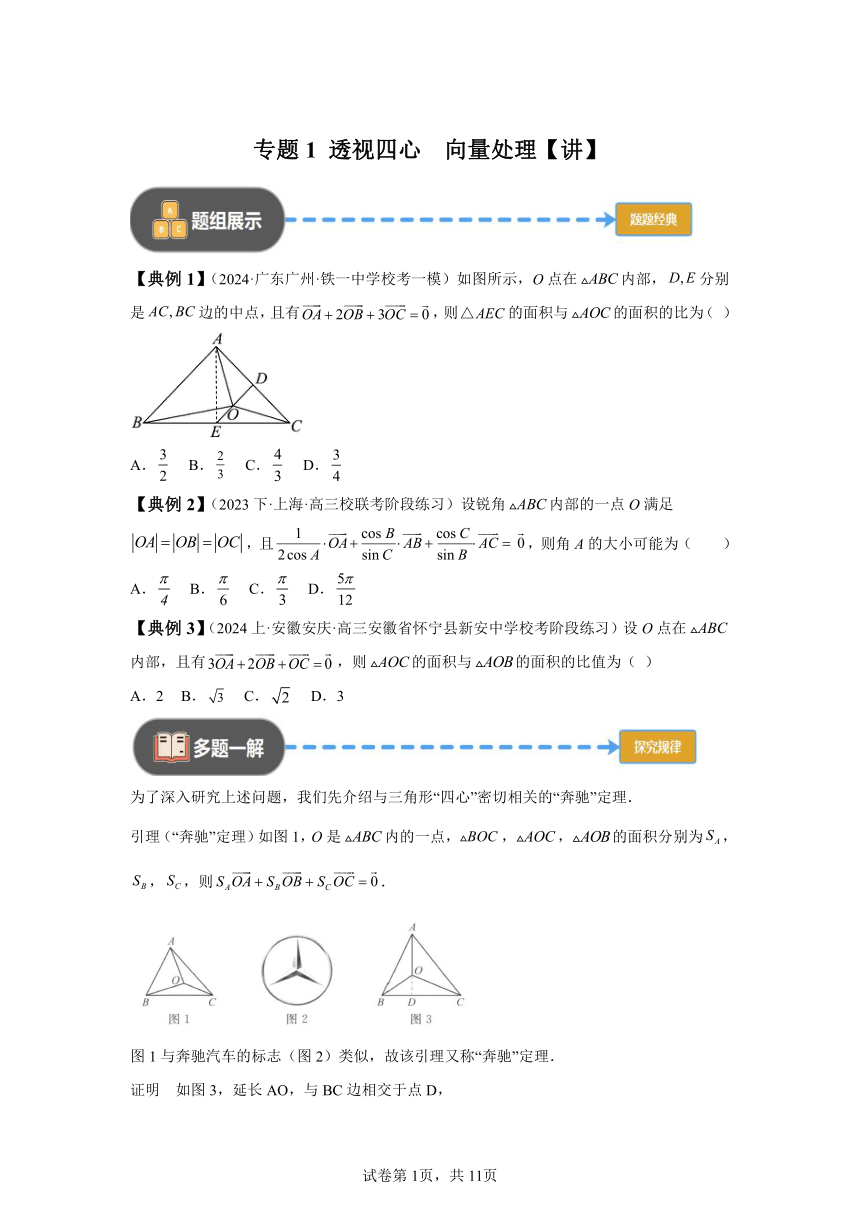
专题1 透视四心 向量处理【讲】 【典例1】(2024·广东广州·铁一中学校考一模)如图所示,O点在内部,分别是边的中点,且有,则的面积与的面积的比为( ) A. B. C. D. 【典例2】(2023下·上海·高三校联考阶段练习)设锐角内部的一点O满足,且,则角A的大小可能为( ) A. B. C. D. 【典例3】(2024上·安徽安庆·高三安徽省怀宁县新安中学校考阶段练习)设O点在内部,且有,则的面积与的面积的比值为( ) A.2 B. C. D.3 为了深入研究上述问题,我们先介绍与三角形“四心”密切相关的“奔驰”定理. 引理(“奔驰”定理)如图1,O是内的一点,,,的面积分别为,,,则. 图1与奔驰汽车的标志(图2)类似,故该引理又称“奔驰”定理. 证明 如图3,延长AO,与BC边相交于点D, 则. 记,则,即, 所以, 又,所以, 从而. 若O是内的一点,且,则. 下面我们归纳三角形“四心”的定义、几何性质和向量特征. 1.重心 ①定义:三角形三条中线的交点. ②几何性质:三角形的重心是中线的三等分点,它到顶点的距离等于它到对边中点距离的2倍. ③向量特征 定理1 G是的重心. 证明由引理得G是的重心. 推论1 P是所在平面内任意一点, 是的重心. 证明 G是的重心 . 注 在推论1中,若P为坐标原点,的三个顶点的坐标分别为,,,则的重心为. 2.外心 ①定义:三角形三条边的中垂线的交点,也是三角形外接圆的圆心. ②几何性质:三角形的外心到三个顶点的距离相等. ③向量特征 定理2 O是锐角的外心. 证明 由O是锐角的外心,得, 则,,, 于是, 根据引理,得到. 反之亦然(证明略). 推论2 P是锐角所在平面内任意一点, 是锐角的外心. 推论2可仿照推论1进行证明. 3.内心 ①定义:三角形三条内角平分线的交点,也是三角形内切圆的圆心. ②几何性质:三角形的内心到三边的距离相等. ③向量特征 定理3 O是的内心(其中a,b,c是的三边长). 证明 设的内切圆半径为r,O是的内心, 则. 根据引理得,O是的内心. 推论3 P是所在平面内任意一点, O是的内心. 推论3 可仿照推论1进行证明. 4.垂心 ①定义:三角形三条高所在直线的交点. ②几何性质:三角形的垂心分每条高线所得的两条线段长的乘积相等. ③向量特征 定理4 O是(非直角三角形)的垂心. 证明O是(非直角三角形)的垂心 , 由引理得,O是(非直角三角形)的垂心. 推论4 P是(非直角三角形)所在平面内任意一点, O是(非直角三角形)的垂心. 推论4可仿照推论1进行证明. 【精细化解析 典例1】 第一步:利用向量运算得三点共线; 由可得, 又因为分别是边的中点,所以,, 所以,即,所以三点共线,且, 第二步:由三角形面积公式即可求解. 所以到的距离与到的距离之比也为, 又的面积与的面积都以为底, 所以的面积与的面积的比为.故选:A [精细化解析 典例2] 第一步:根据三角恒等变换和外心的向量性质,将原式化简; 由于锐角△ABC内部的一点O满足|OA|=|OB|=|OC|, 所以点O为△ABC外接圆的圆心,外接圆的半径为R; 所以 , 整理得 , 第二步:利用数量积的定义二倍角化简求值即可. 所以 , 故 , 则 , 所以 , 故,由于,所以,解得.故选:D. 【精细化解析 典例3】 第一步:设,于是得到点O是的重心; 不妨设,如图所示, 根据题意则,即点O是的重心, 第二步:根据重心性质及高的关系,得到; 取的中点,连接,则三点共线,且, 所以边上的高是边上的高的倍, ,即,同理可得:,, 所以有, 第三步:利用面积关系得结论. 又因为, 那么, 故的面积与的面积的比值为.故选:A. 类型1 由“奔驰”定理演绎三角形面积之比 例1 设点O在内部,且有,D是BC的中点,设与的面积分别为,,则_____. 【详解】 取AC的中点为E,由得, 所以O, ... ...
~~ 您好,已阅读到文档的结尾了 ~~