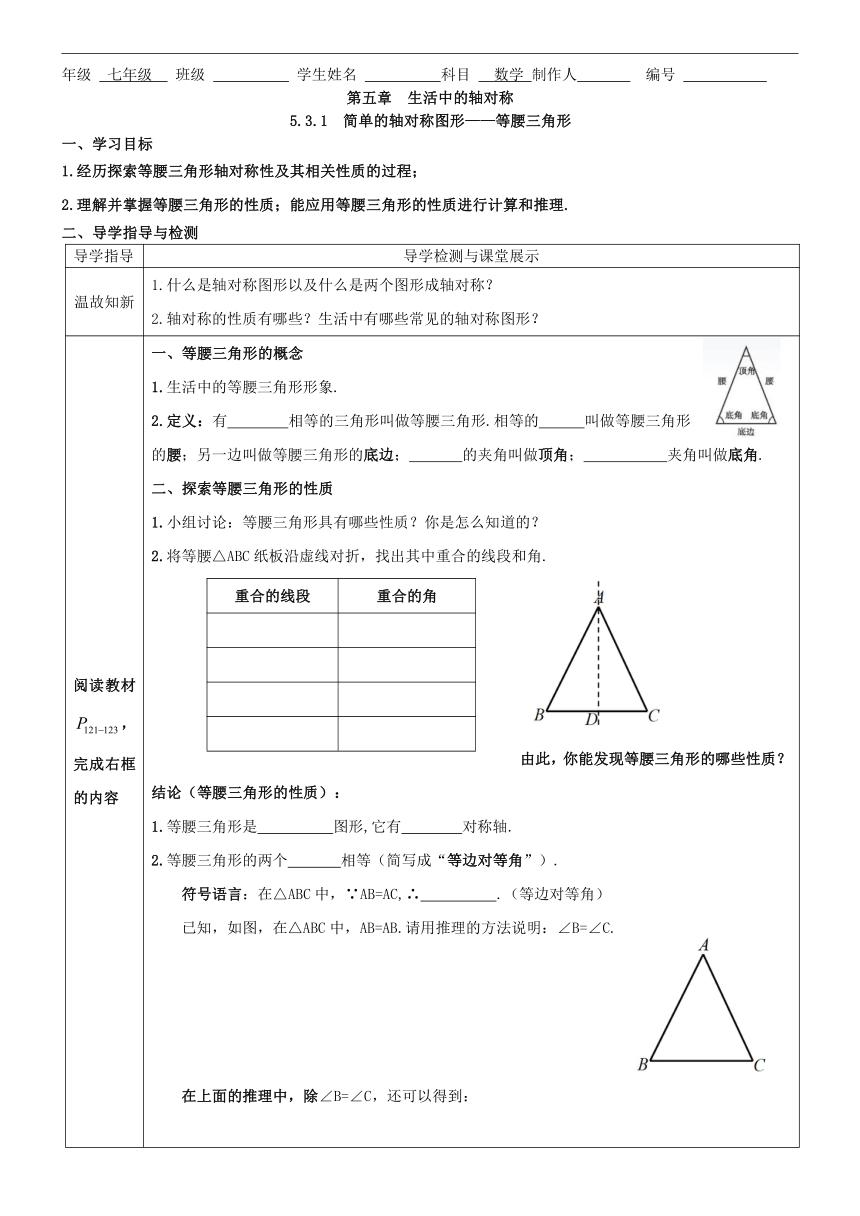
年级 七年级 班级 学生姓名 科目 数学 制作人 编号 第五章 生活中的轴对称 5.3.1 简单的轴对称图形———等腰三角形 一、学习目标 1.经历探索等腰三角形轴对称性及其相关性质的过程; 2.理解并掌握等腰三角形的性质;能应用等腰三角形的性质进行计算和推理. 二、导学指导与检测 导学指导 导学检测与课堂展示 温故知新 1.什么是轴对称图形以及什么是两个图形成轴对称?2.轴对称的性质有哪些?生活中有哪些常见的轴对称图形? 阅读教材,完成右框的内容 一、等腰三角形的概念1.生活中的等腰三角形形象.2.定义:有 相等的三角形叫做等腰三角形.相等的 叫做等腰三角形的腰;另一边叫做等腰三角形的底边; 的夹角叫做顶角; 夹角叫做底角.二、探索等腰三角形的性质1.小组讨论:等腰三角形具有哪些性质?你是怎么知道的?2.将等腰△ABC纸板沿虚线对折,找出其中重合的线段和角.重合的线段重合的角由此,你能发现等腰三角形的哪些性质?结论(等腰三角形的性质):1.等腰三角形是 图形,它有 对称轴.2.等腰三角形的两个 相等(简写成“等边对等角”).符号语言:在△ABC中,∵AB=AC,∴ .(等边对等角)已知,如图,在△ABC中,AB=AB.请用推理的方法说明:∠B=∠C.在上面的推理中,除∠B=∠C,还可以得到:3.等腰三角形 、底边上的 、底边上的 互相重合.(简称“三线合一”)符号语言:(1)∵AB=AC,∠BAD=∠CAD ,∴BD = , ⊥ ;(等腰、顶角平分→中线、高)(2)∵AB=AC,BD=CD ,∴∠BAD= , ⊥ ;;(等腰、中线→顶角平分、高)(3)∵AB=AC,AD⊥BC ,∴∠BAD= ,BD= .(等腰、高→顶角平分、中线)三、等边三角形的性质定义: 都相等的三角形是等边三角形.也叫正三角形.等边三角形的性质: 巩固诊断 A层 1.判断正误:(1)等腰三角形的底角可能是锐角或者直角、钝角. ( ) (2)钝角三角形不可能是等腰三角形.( )(3)等腰三角形的顶角平分线一定垂直于底边. ( ) (4)等腰三角形的顶角一定是锐角.( ) (5)等腰三角形的角平分线、中线和高互相重合.( ) (6)等腰三角形底边上的中线一定平分顶角.( ) 2.等腰三角形的一个内角是50°,则这个三角形的底角的大小是( ) A.65°或50° B.80°或40° C.65°或80° D.50°或80° 3.等腰三角形有一个角是96°,则另两个角分别是 . B层 4.如图,∠O = 15°,且 OA = AB = BC = CD. 则∠1= . 5.等腰三角形的一个内角是50°,则另外两个角的度数分别是( ) A.65° 65° B.50° 80° C.65° 65°或50° 80° D.50° 50° 6.如图,在△ ABC 中, AB = AD = DC ,∠ B =70°,则∠ C 的度 数为( ) A. 35° B. 40° C. 45° D. 50° 7.如果等腰三角形两边长是9cm和4cm,那么它的周长是( )A.17cm B.22cm C.17或22cm D.无法确定 8.一个等腰三角形的底角是顶角的2倍,求它的各个内角的度数. C层 9.已知:如图,在△ABC中,AB=AC,AD是BC上的中线,P是AD上任意一点,连接 PB、 PC,请说明:∠ABP=∠ACP. 10.如图,在△ABC中,AB=AC ,∠A=50°,点D为BC上一点,BF=CD ,CE=BD,求∠EDF的度数. ... ...
~~ 您好,已阅读到文档的结尾了 ~~