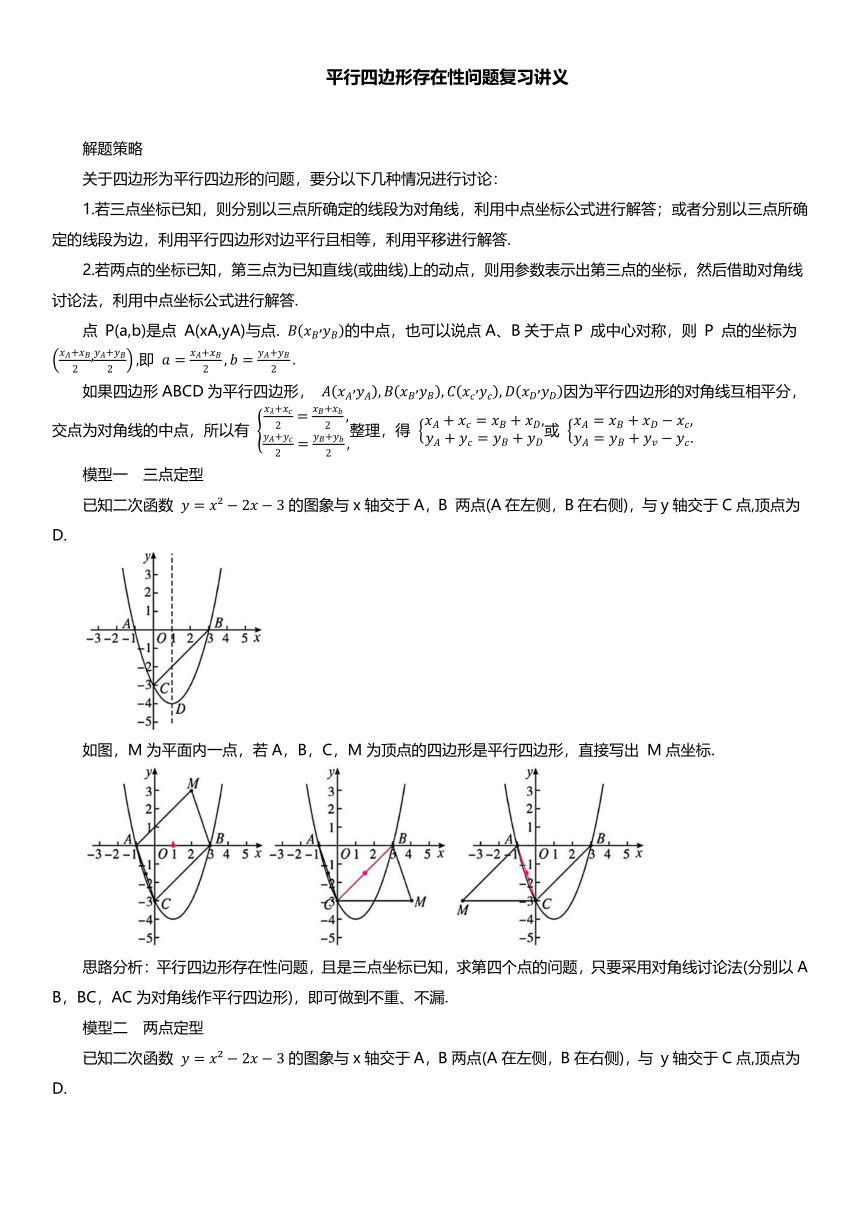
平行四边形存在性问题复习讲义 解题策略 关于四边形为平行四边形的问题,要分以下几种情况进行讨论: 1.若三点坐标已知,则分别以三点所确定的线段为对角线,利用中点坐标公式进行解答;或者分别以三点所确定的线段为边,利用平行四边形对边平行且相等,利用平移进行解答. 2.若两点的坐标已知,第三点为已知直线(或曲线)上的动点,则用参数表示出第三点的坐标,然后借助对角线讨论法,利用中点坐标公式进行解答. 点 P(a,b)是点 A(xA,yA)与点. 的中点,也可以说点A、B关于点P 成中心对称,则 P 点的坐标为 即 如果四边形ABCD为平行四边形, 因为平行四边形的对角线互相平分,交点为对角线的中点,所以有 整理,得 或 模型一 三点定型 已知二次函数 的图象与x轴交于A,B 两点(A在左侧,B在右侧),与y轴交于C点,顶点为 D. 如图,M为平面内一点,若A,B,C,M为顶点的四边形是平行四边形,直接写出 M点坐标. 思路分析:平行四边形存在性问题,且是三点坐标已知,求第四个点的问题,只要采用对角线讨论法(分别以AB,BC,AC为对角线作平行四边形),即可做到不重、不漏. 模型二 两点定型 已知二次函数 的图象与x轴交于A,B两点(A在左侧,B在右侧),与 y轴交于C点,顶点为 D. 如图,M是x轴上一动点,N 是抛物线上一动点.若以A,C,M,N 为顶点的四边形是平行四边形,直接写出点 M的坐标. 思路分析:平行四边形存在性问题,且是A、C两点坐标已知,求其余两个点的问题,只要采用对角线讨论法(分别以AM,MC,AC为对角线作平行四边形),即可做到不重、不漏. 模型三 一点定型 已知二次函数 的图象与x轴交于A,B两点(A 在左侧,B 在右侧),与y轴交于C点,顶点为 D. 如图,抛物线对称轴与x轴交于点E,M是线段AB 上一动点,且 交抛物线对称轴于点N,P 是抛物线上一点.若以M,N,P,E为顶点的四边形是平行四边形,直接写出点 P 的坐标. 思路分析:平行四边形存在性问题,且是E点坐标已知,求其余三个动点中的一个点的坐标问题,只要采用对角线讨论法(分别以 EM,NE,MN为对角线作平行四边形),即可做到不重、不漏. 模型四 菱形问题 已知二次函数 的图象与x轴交于A,B两点(A在左侧,B在右侧),与y轴交于C点.如图,P 是抛物线对称轴上一动点,Q是坐标系内一点,若四边形 ACQP 是菱形,直接写出点 Q的坐标. 思路分析:将一个等腰三角形沿底边翻折得到的四边形就是菱形,所以只需要将菱形存在性问题转化为等腰三角形存在性问题,再结合平行四边形存在性问题的即可解决. 以 A为顶点,CP 为对角线: 以C为顶点,AP 为对角线: 以 P 为顶点,AC为对角线. 模型五 矩形问题 已知二次函数 的图象与x轴交于A,B两点(A在左侧,B在右侧),与y轴交于点C.如图,P 是抛物线对称轴上一动点,Q是平面内一点,若四边形 ACPQ(按逆时针方向)是矩形,直接写出点 Q的坐标. 思路分析:矩形问题可转化为直角三角形和平行四边形问题来解决,可先确定出直角三角形,再以斜边为对角线补充平行四边形,即可得到矩形.注意字母顺序哦! 以 A 为直角顶点,PC为对角线: 以C为直角顶点,PA为对角线: 以 P 为直角顶点,AC为对角线: 精选例题 例1.如图,抛物线 与x轴交于A,B两点(A在B 的左侧),与y轴交于点 N,过点 A 的直线l: 与y 轴交于点C,与抛物线 的另一个交点为D,已知点 A的坐标为( ,点 D 的坐标为( ,点 P 为抛物线 上一动点(不与点 A,D 重合). (1)求抛物线和直线l的解析式; (2)当点 P 在直线l 上方的抛物线上时,过点 P 作. 轴交直线l 于点E,作 轴交直线l于点 F,求. 的最大值; (3)设M为直线l上的点,探究是否存在点M,使得以点 N,C,M,P 为顶点的四边形为平行四边形 若存在,求出点 M的坐标;若不存在,请说明理由. 解析 (1)将点A,D的坐标分别代入直线和抛物线的解析 ... ...
~~ 您好,已阅读到文档的结尾了 ~~