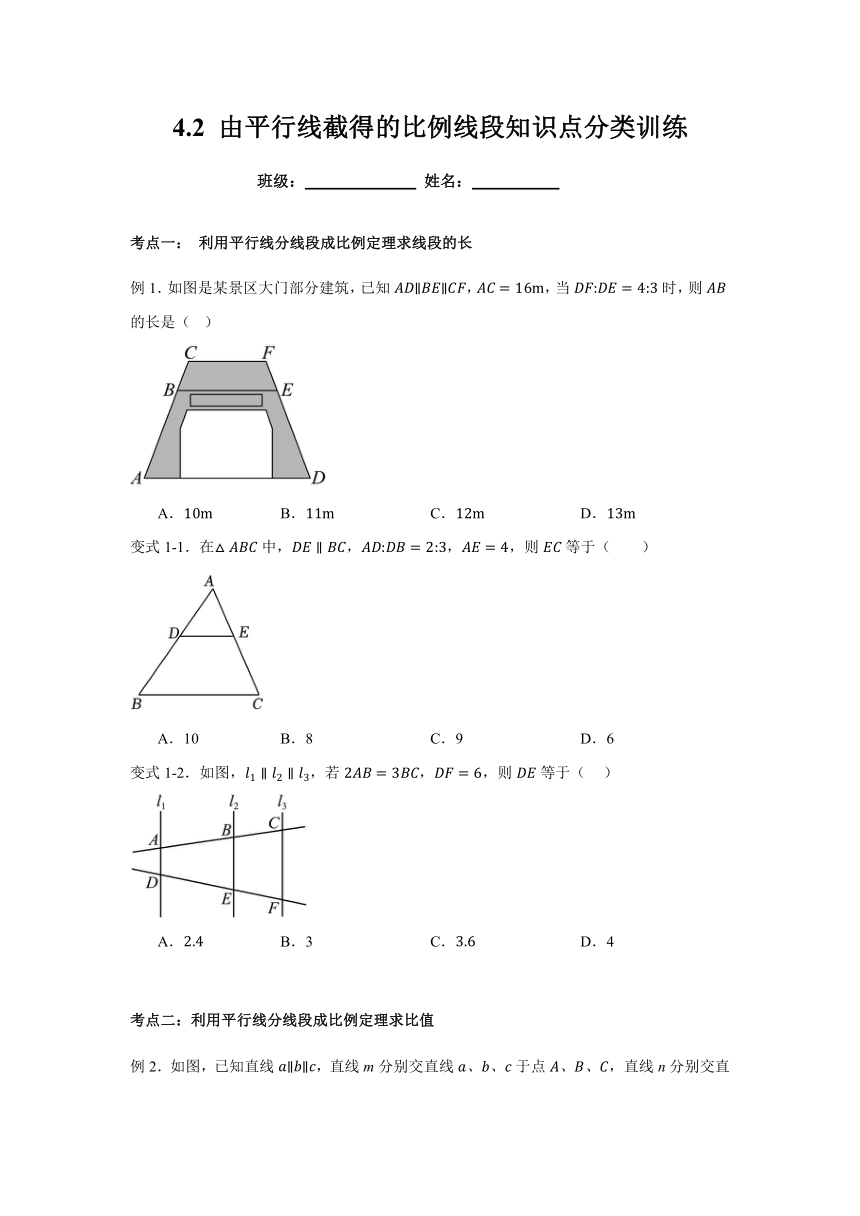
4.2 由平行线截得的比例线段知识点分类训练 班级: 姓名: 考点一: 利用平行线分线段成比例定理求线段的长 例1.如图是某景区大门部分建筑,已知,,当时,则的长是( ) A. B. C. D. 变式1-1.在中,,,,则等于( ) A.10 B.8 C.9 D.6 变式1-2.如图,,若,,则等于( ) A. B.3 C. D.4 考点二:利用平行线分线段成比例定理求比值 例2.如图,已知直线,直线m分别交直线于点直线n分别交直线于点,若,,则的值() A.大于 B.等于 C.小于 D.不能确定 变式2-1.如图,在中,点,分别在,边上,,若,则( ) A. B. C. D. 变式2-2.如图,在中,点D在边上,过点D作,交点E.若,则的值是( ) A. B. C. D. 考点三:构造“A字模型”“X字模型”求线段长或比值 例3.如图,是的中线,点在上,交于点,若,则为( ) A. B. C. D. 变式3-1.如图,在平行四边形中为的中点,为上一点,与交于点,,,,则的长为( ) A. B. C. D. 考点四:平行线分线段成比例在解析几何中应用 例4.如图,在平面直角坐标系中,直线与双曲线交于两点,轴于点,连接交轴于点,结合图象判断下列结论:点与点关于原点对称;点是的中点;在的图象上任取点和点,如果,那么; .其中正确结论的个数是( ) A. B. C. D. 变式4-1.如图,等腰三角形中,,反比例函数的图象经过点A、B及的中点M,轴,与y轴交于点N.则的值为( ) A. B. C. D. 变式4-2.如图,直线交坐标轴于点A,B,交反比例函数于点M,N,若,则k的值为 . 参考答案 考点一: 利用平行线分线段成比例定理求线段的长 例1.如图是某景区大门部分建筑,已知,,当时,则的长是( ) A. B. C. D. 【答案】C 【详解】解:∵, ∴, ∵, ∴, 故选C. 变式1-1.在中,,,,则等于( ) A.10 B.8 C.9 D.6 【答案】D 【详解】解:∵,, ∴, ∵, ∴=, 解得:, 故选:D. 变式1-2.如图,,若,,则等于( ) A. B.3 C. D.4 【答案】C 【详解】解:∵,, ∴, ∴, ∵, ∴, 故选:C. 考点二:利用平行线分线段成比例定理求比值 例2.如图,已知直线,直线m分别交直线于点直线n分别交直线于点,若,,则的值() A.大于 B.等于 C.小于 D.不能确定 【答案】A 【详解】解:作分别交、于、,如图: 可得四边形、四边形为平行四边形, , 直线, ,即, . 故选A. 变式2-1.如图,在中,点,分别在,边上,,若,则( ) A. B. C. D. 【答案】B 【详解】解:∵, , . 故选:B. 变式2-2.如图,在中,点D在边上,过点D作,交点E.若,则的值是( ) A. B. C. D. 【答案】B. 【详解】解:∵, ∴. 故选:B. 考点三:构造“A字模型”“X字模型”求线段长或比值 例3.如图,是的中线,点在上,交于点,若,则为( ) A. B. C. D. 【答案】B 【详解】解:过点作交于点,如图, ∵是的中线, ∴, ∵, ∴, ∵, ∴, ∴, ∴, 故选:B. 变式3-1.如图,在平行四边形中为的中点,为上一点,与交于点,,,,则的长为( ) A. B. C. D. 【答案】B 【详解】解:延长交的延长线于点G,如图所示: ∵四边形是平行四边形, ∴, ∴,, ∵E为的中点, ∴, ∴, ∴, ∵, ∴, ∴, ∵, ∴, 即, 解得:,经检验符合题意. 故选:B. 考点四:平行线分线段成比例在解析几何中应用 例4.如图,在平面直角坐标系中,直线与双曲线交于两点,轴于点,连接交轴于点,结合图象判断下列结论:点与点关于原点对称;点是的中点;在的图象上任取点和点,如果,那么; .其中正确结论的个数是( ) A. B. C. D. 【答案】C 【详解】解:∵直线与双曲线交于两点, ∴点与点关于原点对称,故正确; ∵点与点关于原点 ... ...
~~ 您好,已阅读到文档的结尾了 ~~