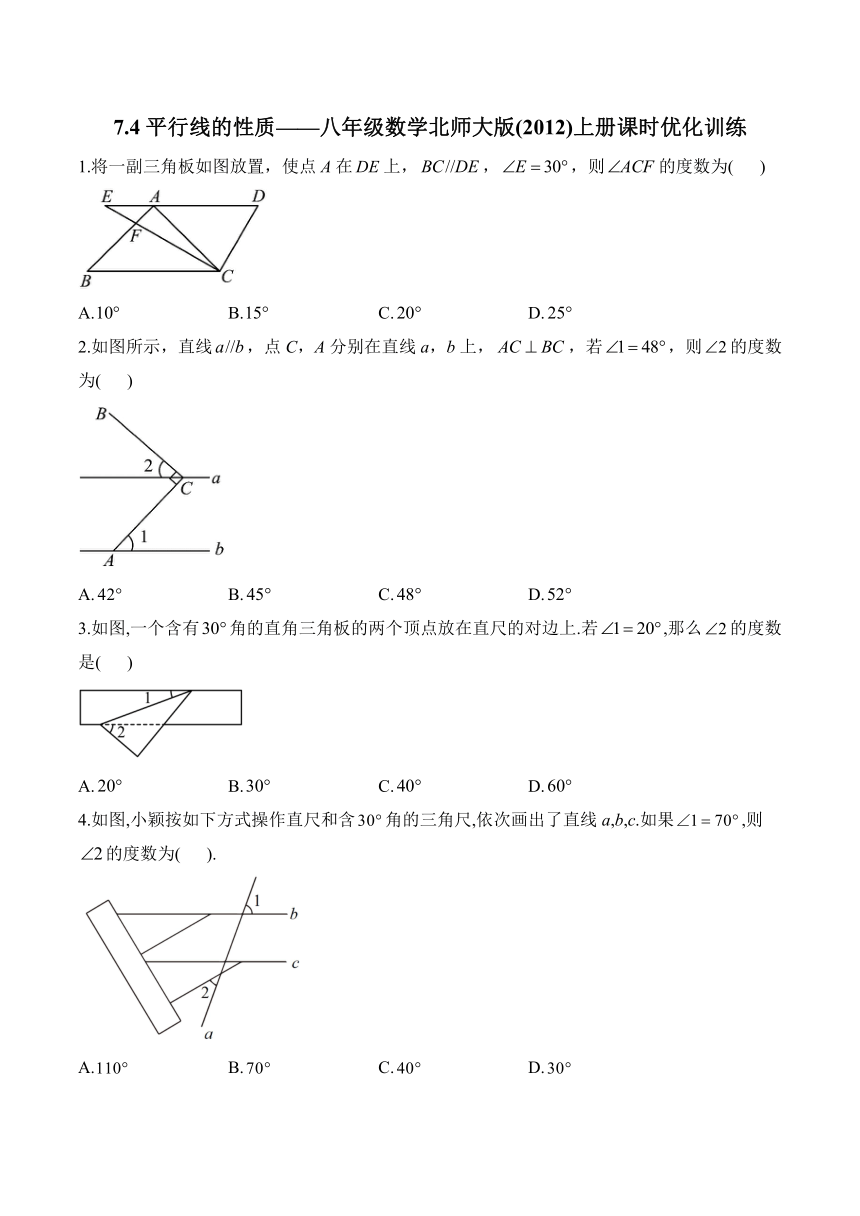
7.4平行线的性质——八年级数学北师大版(2012)上册课时优化训练(含详解)

7.4平行线的性质———八年级数学北师大版(2012)上册课时优化训练 1.将一副三角板如图放置，使点A在上，，，则的度数为( ) A. B. C. D. 2.如图所示，直线，点C，A分别在直线a，b上，，若，则的度数为( ) A. B. C. D. 3.如图,一个含有角的直角三角板的两个顶点放在直尺的对边上.若,那么的度数是( ) A. B. C. D. 4.如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果,则的度数为( ). A. B. C. D. 5.如图,,,则图中与(不包括)相等的角有( ) A.1个 B.2个 C.3个 D.4个 6.传统文化如同一颗璀璨的明珠,熠熠生辉.为增强学生体质,同时让学生感受中国传统文化,某校将国家非物质文化遗产“抖空竹”引入阳光特色大课间.如图①是某同学“抖空竹”时的一个瞬间,小红同学把它抽象成数学问题：如图②,已知,,,则的度数为( ) A. B. C. D. 7.光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,在水中平行的光线,在空气中也是平行的.如下图是从玻璃杯底部发出的一束平行光线经过水面折射形成的光线示意图,水面与玻璃杯的底面平行.若,,则的度数是( ) A. B. C. D. 8.如图,,平分,平分,,则的度数用含的式子表示为( ) A. B. C. D. 9.如图,,,,则_____度. 10.如图，小明从A出发沿北偏东方向行走至B处，又沿北偏西方向行走至C处，此时需把方向调整到与出发时一致，则方向的调整应是右转_____°. 11.一个两边平行的纸条，按下图折叠，则_____ 12.如图,如果、,则_____. 13.如图，已知，，且平分.求证： (1) (2)平分 14.如图,已知,分别探索下列四个图形中与,的关系. (1)如图①,_____；如图②,_____； 如图③,_____；如图④,_____. (2)得到图②结论的过程如下：(补足理由) 过P点作,又∵, ∴(同平行于第三条直线的两直线平行) ∵, ∴_____,_____( ) ∵(图形性质) ∴_____(等量代换) (3)仿照(2),在图③、④中,选一个写出得到结论的过程(给出理由). 答案以及解析 1.答案：B 解析：， ， ， 故选：B. 2.答案：A 解析：如图所示， ∵直线， ∴， ， 故选：A. 3.答案：C 解析：如图, ∵,, ∴, ∴, 故选：C. 4.答案：C 解析：如图, 由题意得：,, , , , , 故选：C. 5.答案：D 解析：∵, ∴； ∵, ∴； ∵, ∴； ∵, ∴； 所以与相等的角有、、、四个, 故选：D 6.答案：C 解析：如图所示,过点E作, ∵, ∴, ∴,, ∴, ∴, 故选：C. 7.答案：C 解析：如图： ∵, , ∵, , , , , 故选：C. 8.答案：B 解析：平分,平分, , 过H作,过E作, , ,,, , 故选：B. 9.答案： 解析：∵,, ∴, ∵, ∴, 故答案为：100. 10.答案： 解析：如图所示： 由题意得：，， ∵， ∴， ， ∵在C处需把方向调整到与出发时一致， ∴， ， ∴ 故答案为：. 11.答案：/50度 解析：根据题意得：，，， ， ， ， . 故答案为：. 12.答案：/180度 解析：∵, ∴, ∴, 同理可得, ∵O在上, ∴, ∴,即, 故答案为：. 13.答案：(1)见解析 (2)见解析 解析：(1)证明：，， ， ， ， ， ， ； (2)证明：平分， ， ， ，， ， ， 平分. 14.答案：(1),,, (2),,两直线平行,内错角相等, (3)选④,结论的过程(理由)见解析 解析：(1)如图①, 过点P作. ∴, ∵, ∴, ∴, ∴ ∴； ∴图①结论：, 过P点作,又∵,如图②； ∴(同平行于第三条直线的两直线平行) ∵, ∴,(两直线平行,内错角相等) ∵(图形性质) ∴(等量代换) 图②结论：, 如图③,过点P作, ∴, ∵,. ∴, ∴, ∴, 即. ∴图③结论：； 如图④,过点P作, ∴, ∵,. ∴, ∴, ∴, 即. 图④结论： (2)过P点作,又∵,如图②； ∴(同平行于第三条直线的两直线平行) ∵, ∴,(两直线平行,内错角相等) ∵(图形性质) ∴(等量代换) (3)如图④,过点P作, ∴, ∵,. ∴, ∴, ∴, 即. ... ...