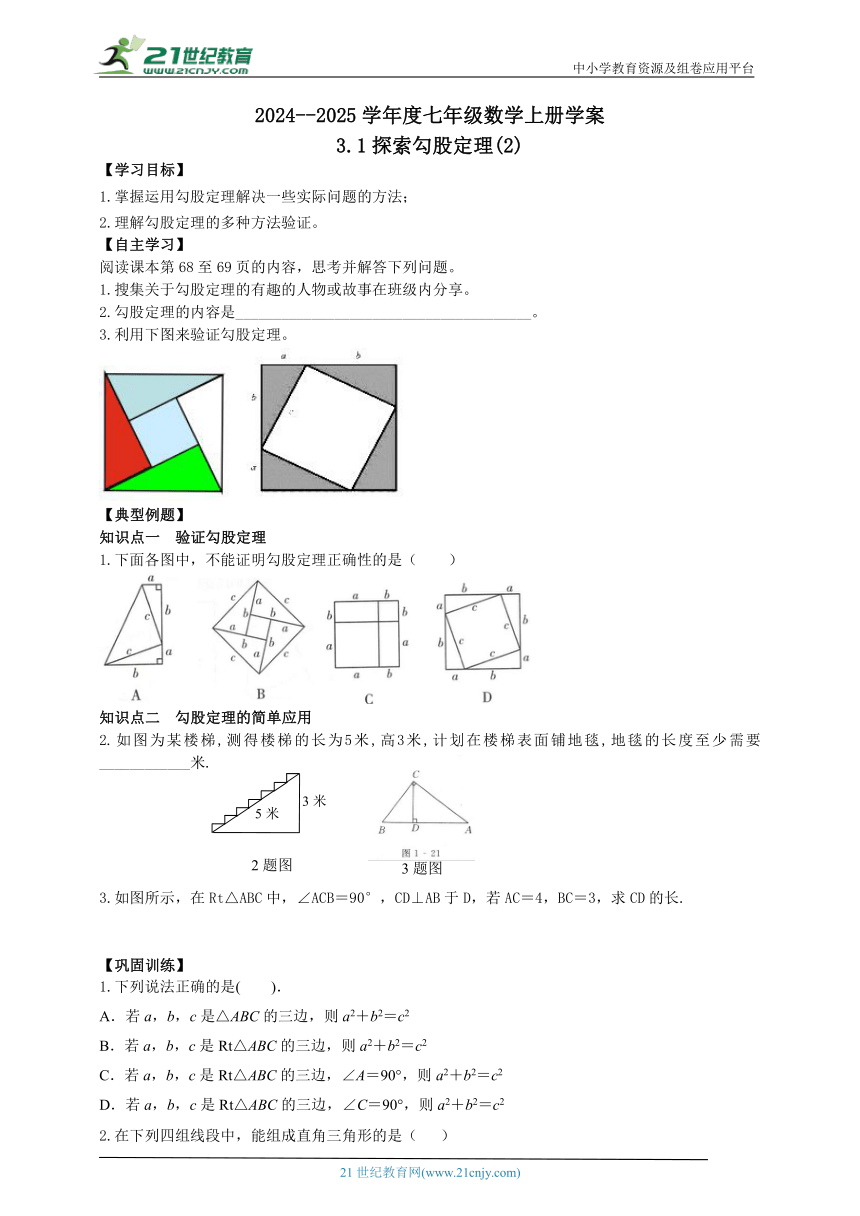
中小学教育资源及组卷应用平台 2024--2025学年度七年级数学上册学案 3.1探索勾股定理(2) 【学习目标】 1.掌握运用勾股定理解决一些实际问题的方法; 2.理解勾股定理的多种方法验证。 【自主学习】 阅读课本第68至69页的内容,思考并解答下列问题。 1.搜集关于勾股定理的有趣的人物或故事在班级内分享。 2.勾股定理的内容是_____。 3.利用下图来验证勾股定理。 【典型例题】 知识点一 验证勾股定理 1.下面各图中,不能证明勾股定理正确性的是( ) 知识点二 勾股定理的简单应用 2.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要_____米. ( 3题图 ) ( 2题图 ) 3.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,BC=3,求CD的长. 【巩固训练】 1.下列说法正确的是( ). A.若a,b,c是△ABC的三边,则a2+b2=c2 B.若a,b,c是Rt△ABC的三边,则a2+b2=c2 C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2 D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2 2.在下列四组线段中,能组成直角三角形的是( ) A.a=32,b=42,c=52 B.a=11、b=12、c=13 C.a=9,b=40,c=41 D.a:b:c=1:1:2 3.在直角三角形ABC中,斜边AB=2,则=_____. 4.一直角三角形的一条直角边长是7cm,另一条直角边与斜边长的和是49cm,则斜边的长( ) A.18cm B.20cm C.24cm D.25cm 5.一直角三角形的两边长分别为3和4,则第三边的长为( ) A.5 B. C. D.5或 【课后拓展】 1.如图1-16所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为 ( ) 2.已知△ABC中,AB=17,AC=10,BC边上的高AD=8,则边BC的长为( ) A.21 B.15 C.6 D.以上答案都不对 3.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积。 ( A B C D 第 3 题图 ) 3.1探索勾股定理(2) 【自主学习】 略; 直角三角形两条直角边的平方和等于斜边的平方; 略; 【典型例题】 1.略(提示:以梯形面积为等量关系来列等式) 2.7 3.540千米/小时 【巩固训练】 1.(1)13(2)8(3)6;8 2.C 3.8 4.D 【课后拓展】 1.49 2.36cm2 21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页) 21世纪教育网(www.21cnjy.com)
~~ 您好,已阅读到文档的结尾了 ~~