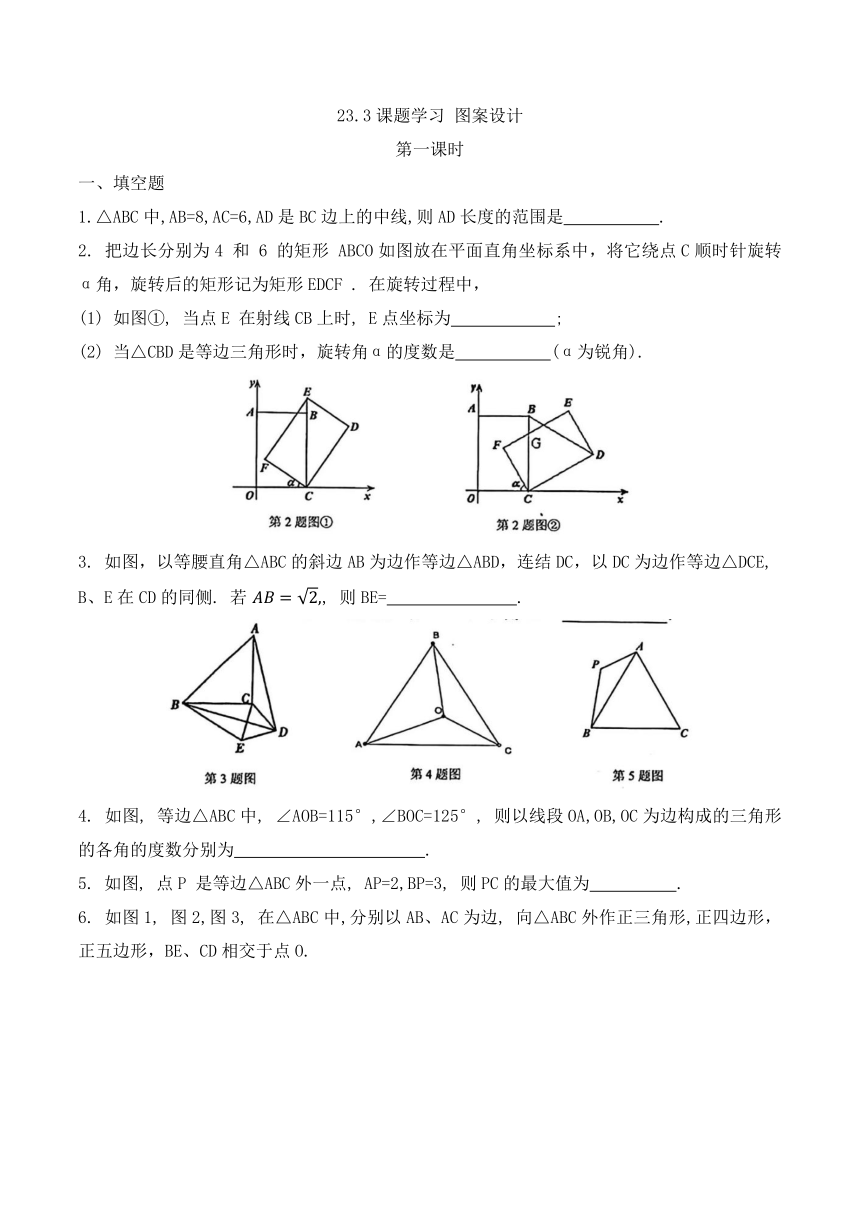
23.3课题学习 图案设计 课时练习（3课时、无答案） 人教版数学九年级上册

23.3课题学习 图案设计 第一课时 一、填空题 1.△ABC中,AB=8,AC=6,AD是BC边上的中线,则AD长度的范围是 . 2. 把边长分别为4 和 6 的矩形 ABCO如图放在平面直角坐标系中，将它绕点C顺时针旋转α角，旋转后的矩形记为矩形EDCF . 在旋转过程中， (1) 如图①, 当点E 在射线CB上时, E点坐标为 ; (2) 当△CBD是等边三角形时，旋转角α的度数是 (α为锐角). 3. 如图，以等腰直角△ABC的斜边AB为边作等边△ABD，连结DC，以DC为边作等边△DCE, B、E在CD的同侧. 若 , 则BE= . 4. 如图, 等边△ABC中, ∠AOB=115°,∠BOC=125°, 则以线段OA,OB,OC为边构成的三角形的各角的度数分别为 . 5. 如图, 点P 是等边△ABC外一点, AP=2,BP=3, 则PC的最大值为 . 6. 如图1, 图2,图3, 在△ABC中,分别以AB、AC为边, 向△ABC外作正三角形,正四边形，正五边形，BE、CD相交于点O. (1) 如图1, ∠BOC=; 如图2, ∠BOC=; 如图3, (2)如图4, 已知: AB、AD是以AB为边向△ABC外所作正n边形的一组邻边; AC、AE是以AC为边向△ABC外所作正n边形的一组邻边. BE、CD的延长线交于点O. 此时, ∠BOC= (用含n的式子表示). 二、选择题 7. 如图，将正方形图案绕中心O旋转180°后，得到的图案是 ( ). 8. 如图,△ ABC中, AD是∠BAC内的一条射线, BE⊥AD, 且△ CHM可由△ BEM旋转而得，则下列结论中错误的是( ) A. M 是BC的中点 C. CF⊥AD D. FM⊥BC 9. 如图, C是线段BD上一点, 分别以BC,CD为边作等边△ABC和等边△CDE,AD交CE于F，BE交AC于G ，则图中可通过旋转而相互得到的三角形对数有( ). A. 1对B. 2对 C. 3对 D. 4对 10.如图,在平面直角坐标系中,△ABC和△DEF为等边三角形, AB=DE,点B、C、D在x轴上, 点A、 E、 F在y轴上, 下面判断正确的是( ). A. △DEF 是△ABC绕点O顺时针旋转90°得到的 B. △DEF 是△ABC绕点O逆时针旋转90°得到的 C. △DEF 是△ABC绕点O顺时针旋转60°得到的 D. △DEF 是△ABC绕点O顺时针旋转120°得到的 11. 如图, 将等腰Rt△ABC绕点A 逆时针旋转 15°得到△AB'C', 若AC=1, 则图中阴影部分面积为( ) A.2 B. 12. 如图, 将△ABC绕点C(0,-1)旋转180°得到△A'B'C,设点 A的坐标为(a,b)则点 A'的坐标为 ( ). A. (-a,-b) B. (-a,-b-1) C. (-a,-b-2) D. (-a,-b+1) 三、解答题 13. 如图, 菱形ABCD中, ∠B=60°, 若∠EAF=60°. 求证: △AEF是等边三角形. 14. 点P为等边 内一点，若 求 的度数及 的面积. 15. 点D是 的边AC上一点，且 , 点E是BD的中点,若 求BC的长. 第二课时 一、填空题 1. 如图, 已知正方形ABCD的边长为3, E为CD边上一点, DE=1. 以点A为中心,把△ADE 顺时针旋转90°, 得△ABE', 连接EE', 则EE'的长等于 . 2.如图，边长为6的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF交AD于点H, 那么DH 的长为 . 3. 如图, 在正方形ABCD中, E为DC边上的点,连结BE, 将△BCE绕点C顺时针方向旋转90°得到△DCF, 连结EF, 若∠BEC=60°, 则∠EFD为 度. 4.如图, E、F 分别是正方形ABCD的边BC、CD上的点, BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向转到△BCF ，旋转角为( 则∠α= . 5. 如图,已知△ABC中, AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE, PF分别交AB, AC于点E, F, 给出以下五个结论: ①AE=CF②∠APE=∠CPF③△EPF是等腰直角三角形④ 当∠EPF在△ABC内绕顶点P旋转时(点E不与A，B重合)，上述结论中始终正确的序号有 . 6.如图,四边形ABCD中,∠DAB=∠BCD=90°,CD=CB,AC=，则四边形ABCD的面积为 . 7. 如图，将正方形 ABCD 以点 B 为旋转中心顺时针旋转 120°得到正方形A'BC'D',DO⊥C'A'于O,若 则正方形ABCD的边长为 . 8.如图，在直角梯形ABCD中，AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点, 且∠DCE=45°,BE=4, 则DE= . 二、选择题 ... ...