13.1.1轴对称 同步练习（无答案）

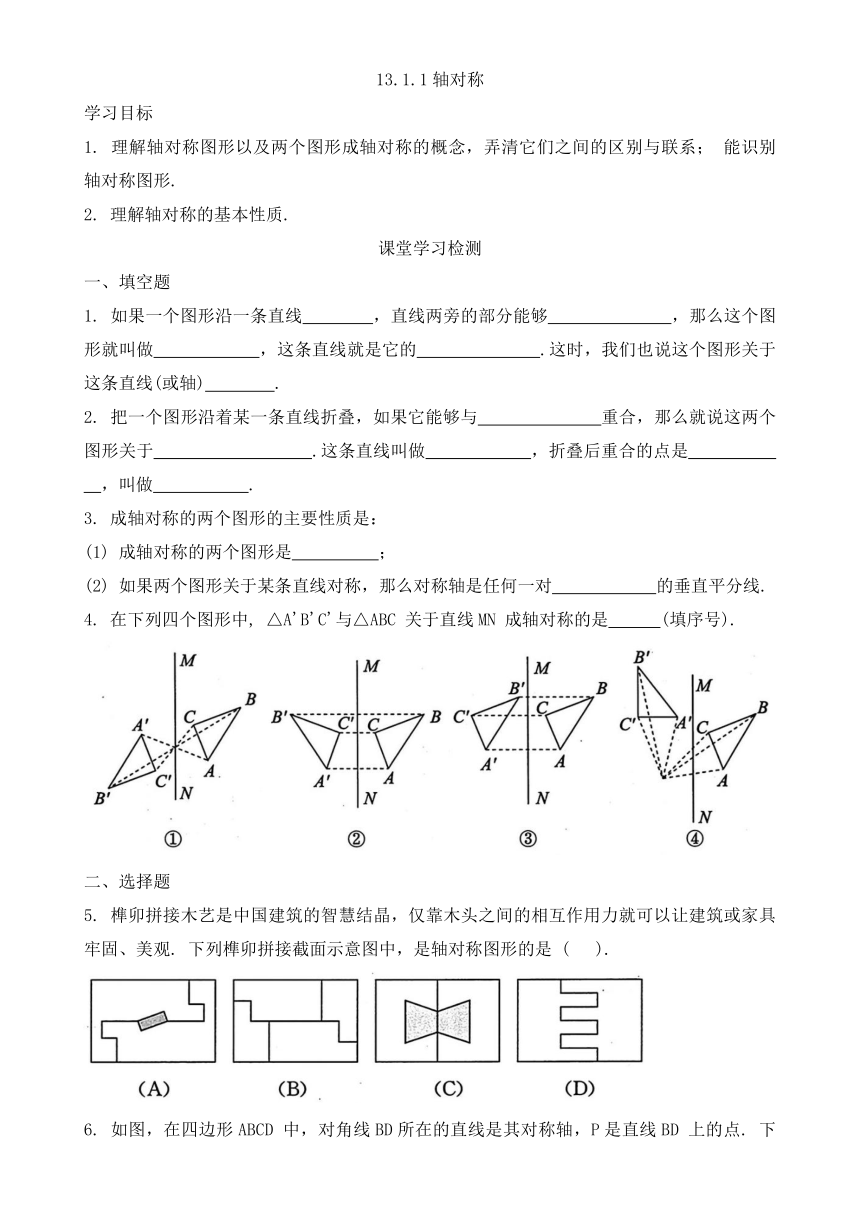
13.1.1轴对称 学习目标 1. 理解轴对称图形以及两个图形成轴对称的概念，弄清它们之间的区别与联系； 能识别轴对称图形. 2. 理解轴对称的基本性质. 课堂学习检测 一、填空题 1. 如果一个图形沿一条直线 ，直线两旁的部分能够 ，那么这个图形就叫做 ，这条直线就是它的 .这时，我们也说这个图形关于这条直线(或轴) . 2. 把一个图形沿着某一条直线折叠，如果它能够与 重合，那么就说这两个图形关于 .这条直线叫做 ，折叠后重合的点是 ，叫做 . 3. 成轴对称的两个图形的主要性质是： (1) 成轴对称的两个图形是 ； (2) 如果两个图形关于某条直线对称，那么对称轴是任何一对 的垂直平分线. 4. 在下列四个图形中, △A'B'C'与△ABC 关于直线MN 成轴对称的是 (填序号). 二、选择题 5. 榫卯拼接木艺是中国建筑的智慧结晶，仅靠木头之间的相互作用力就可以让建筑或家具牢固、美观. 下列榫卯拼接截面示意图中，是轴对称图形的是 ( ). 6. 如图，在四边形ABCD 中，对角线BD所在的直线是其对称轴，P是直线BD 上的点. 下列结论中，错误的是 ( ). (A) AD=CD (B) AP=BC (C) ∠DAP=∠DCP (D) ∠ABP=∠CBP 7. 如图, △ABC与△A'B'C'关于直线l对称,则∠B等于 ( ). (A) 30° (B) 50° (C) 90° (D) 100° 8. 如图，将一张正方形纸片按如图1、图2所示的方式对折，然后沿图3中的虚线剪裁得到图4，将图4的纸片展开铺平，再得到的图案是 ( ). 综合·运用·诊断 填空题 9. 下列图形均为正多边形，画出它们的所有对称轴，并填空. 10. 在△ABC中,将∠B, ∠C按如图所示的方式折叠, 点 B,C均落在边 BC上的点Q处, MN, EF为折痕. 若∠A=82°, 则∠MQE的度数为 . 11. 如图, 在△ABC中,∠ACB=90°,∠A=50°. 将其折叠, 使点A落在边CB 上, 落点记为A', 折痕为CD, 则∠A'DB= °. 12. 如图, 在长方形 ABCD 中, AB=12cm, BC=6cm, 点 E, F分别在AB, CD上. 将长方形ABCD沿EF折叠并压平，使点A，D分别落在长方形ABCD外部，落点分别记为A'，D'，则整个阴影部分图形的周长为 cm. 拓展·探究·思考 解答题 13. 图1是4×4的正方形网格，其中已有3个小方格被涂成了黑色. 现在要从其余13个白色小方格中选出一个也涂成黑色，使整个涂成黑色的图形成为轴对称图形，请在下图中补全图形. 可能的位置有几种 请在图中用阴影标出，并画出对称轴.