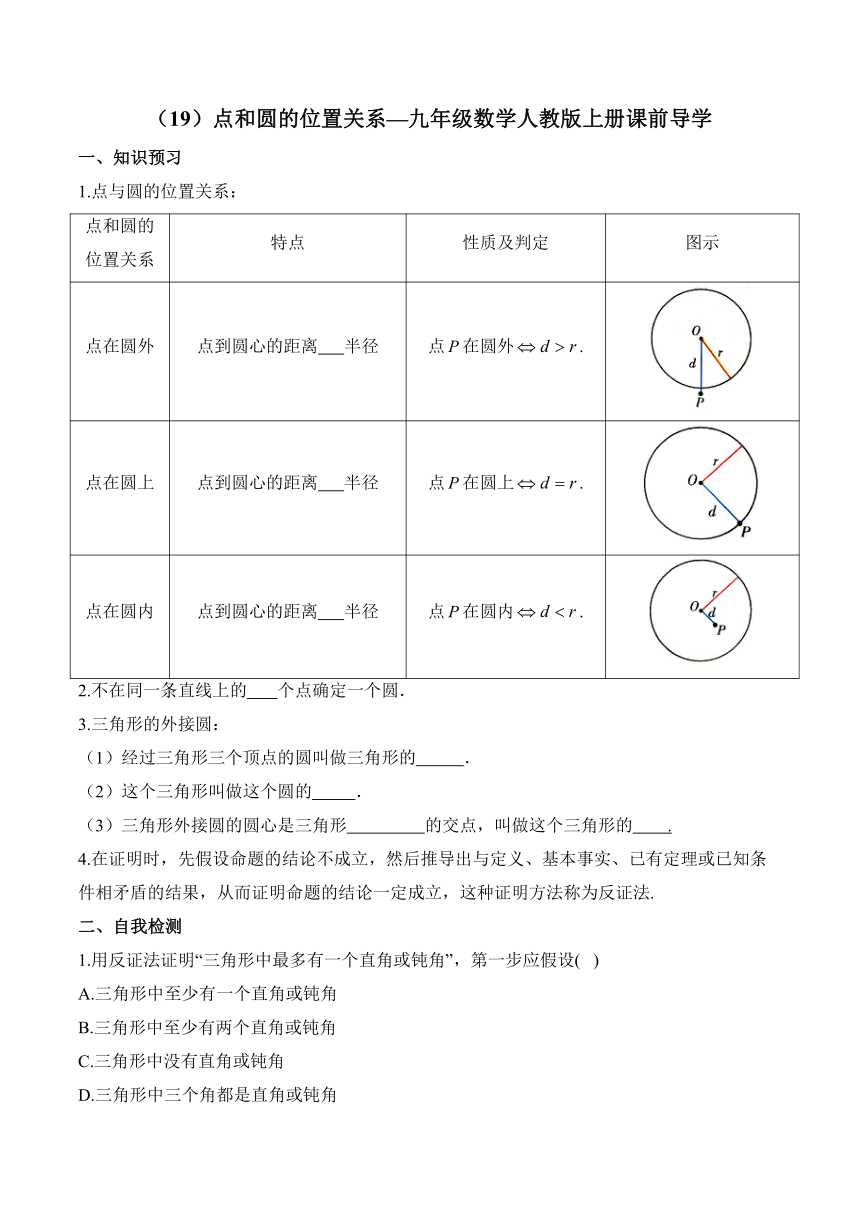
（19）点和圆的位置关系—九年级数学人教版上册课前导学（含答案）

（19）点和圆的位置关系—九年级数学人教版上册课前导学 一、知识预习 1.点与圆的位置关系： 点和圆的位置关系 特点 性质及判定 图示 点在圆外 点到圆心的距离 半径 点在圆外. 点在圆上 点到圆心的距离 半径 点在圆上. 点在圆内 点到圆心的距离 半径 点在圆内. 2.不在同一条直线上的 个点确定一个圆． 3.三角形的外接圆： （1）经过三角形三个顶点的圆叫做三角形的 ． （2）这个三角形叫做这个圆的 ． （3）三角形外接圆的圆心是三角形 的交点，叫做这个三角形的 . 4.在证明时，先假设命题的结论不成立，然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果，从而证明命题的结论一定成立，这种证明方法称为反证法. 二、自我检测 1.用反证法证明“三角形中最多有一个直角或钝角”，第一步应假设( ) A.三角形中至少有一个直角或钝角 B.三角形中至少有两个直角或钝角 C.三角形中没有直角或钝角 D.三角形中三个角都是直角或钝角 2.如图2，在平面直角坐标系中，点A，B，C的坐标为、、，则外接圆的圆心坐标是( ) A. B. C. D. 3.如图,在的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( ) A.点P B.点Q C.点R D.点M 4.已知的半径为，若点A到圆心O的距离为，则点A( ) A.在内 B.在上 C.在外 D.与的位置关系无法确定 5.已知平面直角坐标系xOy中,的半径是10,则点与的位置关系是( ) A.点P在内 B.点P在上 C.点P在外 D.无法确定 6.在中，，，，如果以点A为圆心，AC为半径作，那么斜边AB的中点D在_____.(填“内”、“上”或者“外”) 7.已知平面直角坐标系中的三个点分别为，则A、B、C这三个点_____确定一个圆（填“可以”或“不可以”）. 8.如图,在平面直角坐标系中,一段圆弧经过格点A,B,C,点O为坐标原点(网格纸中每个小正方形的边长为1). (1)该图中弧所在圆的圆心D的坐标为_____. (2)根据(1)中的条件填空： ①的半径_____.(结果保留根号)； ②点在_____.(填“上”、“内”或“外”)； ③_____. 答案以及解析 一、知识预习 1.大于 等于 小于 2.三 3. 外接圆 内接三角形 垂直平分线 外心 二、自我检测 1.答案：B 解析：用反证法证明“三角形中最多有一个直角或钝角”， 第一步应假设三角形中至少有两个直角或钝角， 故选：B. 2.答案：D 解析：根据垂径定理的推论，则 作弦AB、AC的垂直平分线，交点即为圆心，且坐标是. 故选：D. 3.答案：B 解析：作AB的垂直平分线,作BC的垂直平分线,如图, 它们都经过Q,所以点Q为这条圆弧所在圆的圆心. 故选：B. 4.答案：A 解析：的半径为，若点A到圆心O的距离为，， 点A在内， 故选：A. 5.答案：B 解析：点P的坐标是,由勾股定理可得. 又半径是10, 点P在上. 故选:B. 6.答案：上 解析：，，，， 半径为2， 斜边AB的中点D在上， 故答案是：上. 7.答案：可以 解析：设直线的解析式为， 把，代入得， ， 解得，， 所以直线的解析式为， 当时，， 所以点不在直线上， 即点A、B、C不在同一条直线上， 所以过A、B、C这三个点能确定一个圆. 故答案为：可以 8.答案：(1) (2)①；②外；③ 解析：(1)如图,作线段和线段的垂直平分线,则两直线交点即为圆心D, ∴由图可知圆心D的坐标为. 故答案为：； (2)①由图可知的半径. 故答案为：； ②∵点到圆心D的距离为, ∴点在外. 故答案为：外； ③如图,连接, ∵,, ∴, ∴. 故答案为：. ... ...