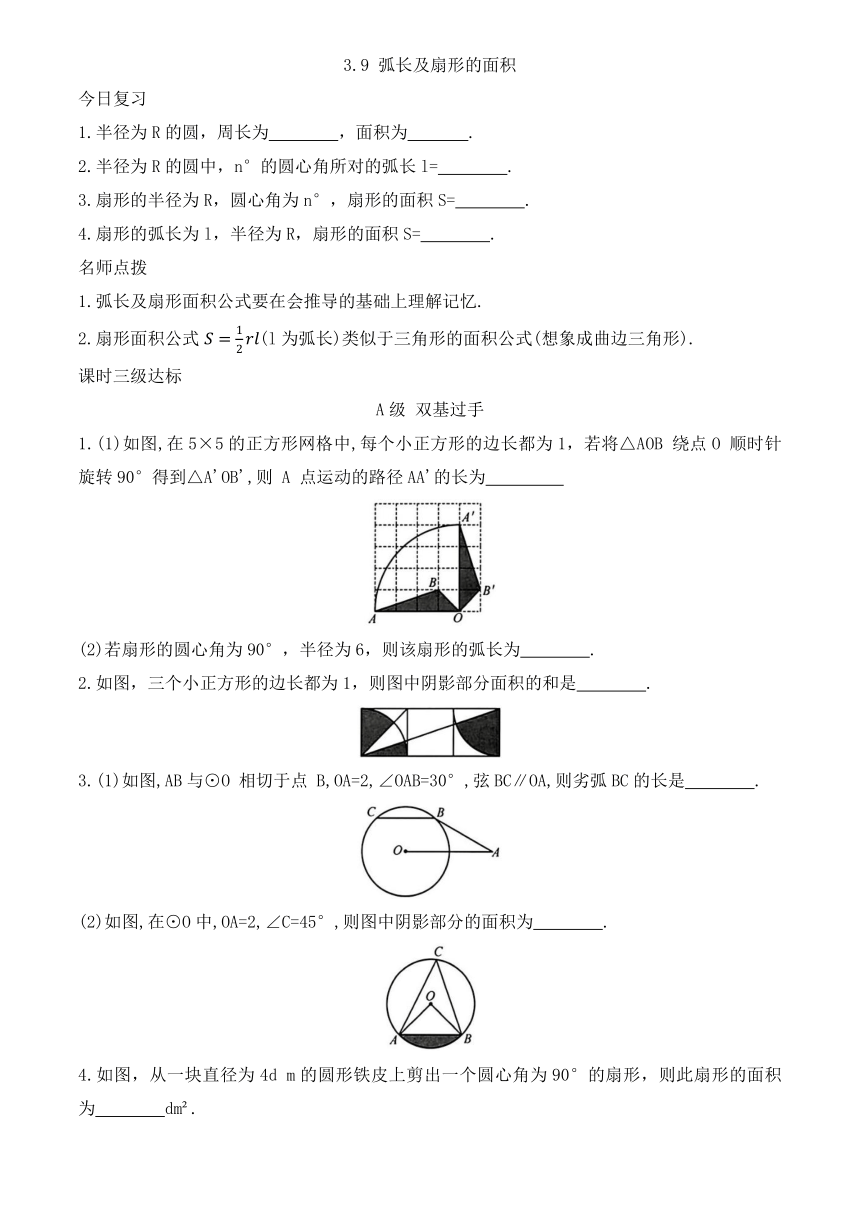
3.9 弧长及扇形的面积 今日复习 1.半径为R的圆,周长为 ,面积为 . 2.半径为R的圆中,n°的圆心角所对的弧长l= . 3.扇形的半径为R,圆心角为n°,扇形的面积S= . 4.扇形的弧长为l,半径为R,扇形的面积S= . 名师点拨 1.弧长及扇形面积公式要在会推导的基础上理解记忆. 2.扇形面积公式 (l为弧长)类似于三角形的面积公式(想象成曲边三角形). 课时三级达标 A级 双基过手 1.(1)如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB 绕点O 顺时针旋转90°得到△A'OB',则 A 点运动的路径AA'的长为 (2)若扇形的圆心角为90°,半径为6,则该扇形的弧长为 . 2.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 . 3.(1)如图,AB与⊙O 相切于点 B,OA=2,∠OAB=30°,弦BC∥OA,则劣弧BC的长是 . (2)如图,在⊙O中,OA=2,∠C=45°,则图中阴影部分的面积为 . 4.如图,从一块直径为4d m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为 dm . 5.120°的圆心角所对的弧长是6π,则此弧所在圆的半径是 ( ) A.3 B.4 C.9 D.18 6.如图,正六边形ABCDEF 的边长为6,以顶点A 为圆心,AB的长为半径画圆,则图中阴影部分的面积为 ( ) A.4π B.6π C.8π D.12π 7.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则AC的长为 ( ) A.2π B.π C. D. 8.如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰好在 EF上,设. ,当α由小到大变化时,图中阴影部分的面积 ( ) A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大,后由大到小 9.(1)如图,在矩形 ABCD中, 2,以点 A为圆心、AD 的长为半径画弧交边BC 于点E,连接AE,求 的长度. (2)如图,已知点O是正六边形ABCDEF的中心,扇形 AOE 的面积是12π,求该正六边形的边长. 10.(1)如图,⊙O是正六边形ABCDEF 的外接圆,正六边形的边长为 ,求阴影部分的面积 (2)如图,在 中, ⊙O与BC,AC分别相切于点E,F,BO平分 连接OA. ①求证:AB是⊙O的切线; ②若 ⊙O的半径是 1,求图中阴影部分的面积. B级 能力提升 11.(1)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是A,B,C,如果 AB=1,那么曲线 CDEF 的长是 . (2)如图,半圆O的直径AB=2,弦CD∥AB,∠COD = 90°, 则图中 阴影 部分 的面 积为 12.如图,半径为1的圆O与正五边形ABCDE相切于点 A,C,劣弧 AC的长度为 . 13.如图,AB是半圆O 的直径,且 C为半圆上的一点.将此半圆沿 BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是 .(结果保留π) 14.如图,在 中, 将 绕点C 顺时针旋转 此时点 B 恰好在DE 上,其中点A经过的路径为弧AD,求图中阴影部分的面积. C级 综合拓展 15.如图,在 中,O 是AB 边上一点, ,过点 A 的⊙O切BC 于点 D,CO平分 (1)求证:AC 是⊙O的切线; (2)若 求⊙O的半径长; (3)在(2)的条件下,求阴影部分的面积. ... ...
~~ 您好,已阅读到文档的结尾了 ~~