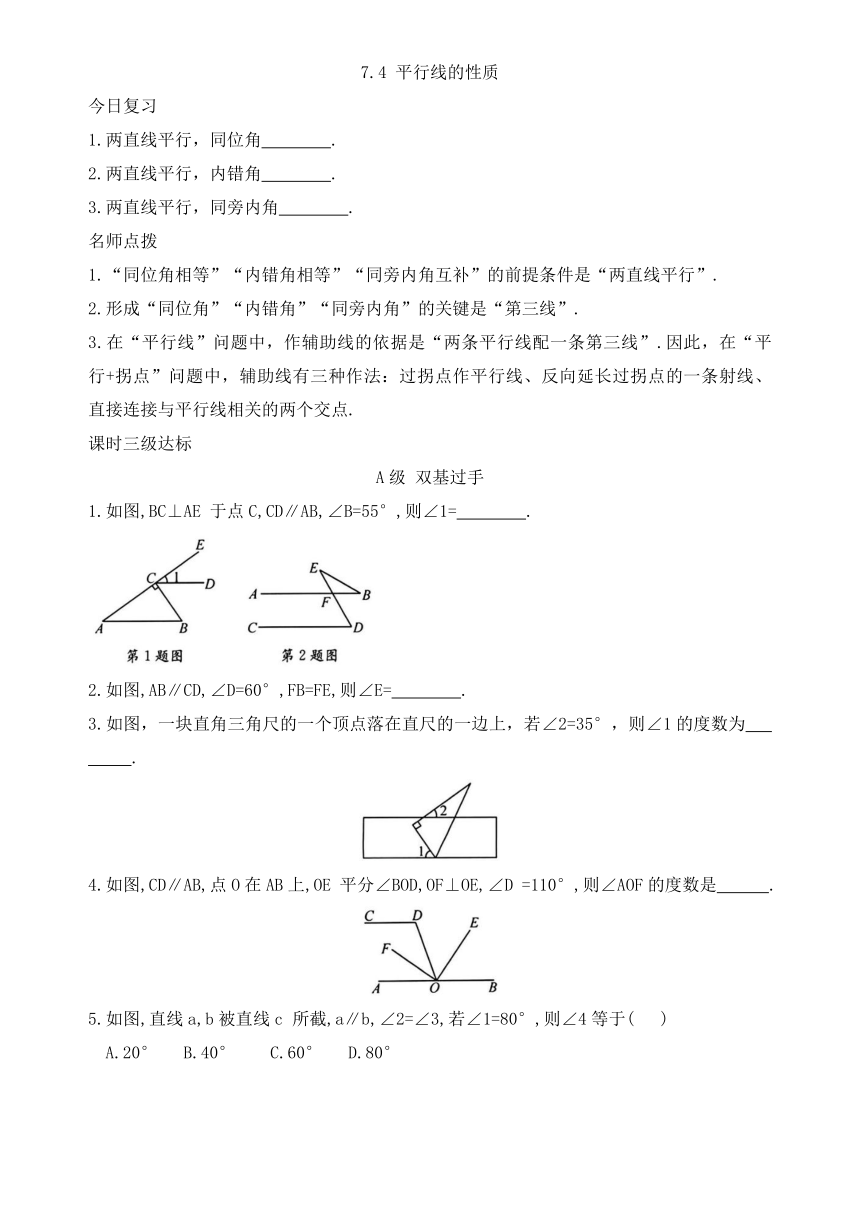
7.4 平行线的性质 今日复习 1.两直线平行,同位角 . 2.两直线平行,内错角 . 3.两直线平行,同旁内角 . 名师点拨 1.“同位角相等”“内错角相等”“同旁内角互补”的前提条件是“两直线平行”. 2.形成“同位角”“内错角”“同旁内角”的关键是“第三线”. 3.在“平行线”问题中,作辅助线的依据是“两条平行线配一条第三线”.因此,在“平行+拐点”问题中,辅助线有三种作法:过拐点作平行线、反向延长过拐点的一条射线、直接连接与平行线相关的两个交点. 课时三级达标 A级 双基过手 1.如图,BC⊥AE 于点C,CD∥AB,∠B=55°,则∠1= . 2.如图,AB∥CD,∠D=60°,FB=FE,则∠E= . 3.如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=35°,则∠1的度数为 . 4.如图,CD∥AB,点O在AB上,OE 平分∠BOD,OF⊥OE,∠D =110°,则∠AOF的度数是 . 5.如图,直线a,b被直线c 所截,a∥b,∠2=∠3,若∠1=80°,则∠4等于( ) A.20° B.40° C.60° D.80° 6.如图,AB∥CD,BE交AD于点E,若∠B=18°,∠D=32°,则∠BED的度数为 ( ) A.18° B.32° C.50° D.60° 7.如图,已知 DE∥BC,如果∠1=70°,那么∠B的度数为 ( ) A.70° B.100° C.110° D.120° 8.将一副直角三角板(∠A=∠FDE=90°,∠F=45°,∠C=60°,点 D在边AB上)按图中所示位置摆放,两条斜边为EF,BC,且EF∥BC,则∠ADF等于( ) A.70° B.75° C.80° D.85° 9.(1)如图,直线 AB 于点 D, 求 的度数. (2)如图, 62°, EG 平分求∠CEF 的度数. 10.已知: (1)如图1,求证: (2)如图2,当 时,请直接写出与 互余的角. B级 能力提升 11.如图,直线a∥b,将一块含 30°角 的直角三角尺按图中方式放置,其中A,C两点分别落在直线a 和b上.若∠1=20°,则∠2的度数为 . 12.如图,AD∥BC,P 是射线BC 上一动点,且不与点 B重合. AM,AN分别平 分 ∠BAP,∠DAP, ∠B =α,∠BAM=β,在点 P 运动的过程中,当∠BAN= ∠BMA 时, 13.如图,C 是直线AB,DE之间的一点, 有下列条件:①∠α+∠β=180°;②∠β-∠α=90°;③∠β=3∠α;④∠α+∠β=90°.其中能使得AB‖DE的是 (填序号). 14.如图,正六边形 内部有一个正五边形 且 直线l经过点 求直线l与 的夹角α. C级 综合拓展 15.已知直线 EF 分别与直线AB,CD 相交于点G,H,并且∠AGE+ (1)如图1,求证:AB∥CD; (2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+ (3)如图3,在(2)的条件下,射线 GH 是 的平分线,在MH 的延长线上取点N, 连接 GN, 若 ∠N = 求 的度数.
~~ 您好,已阅读到文档的结尾了 ~~