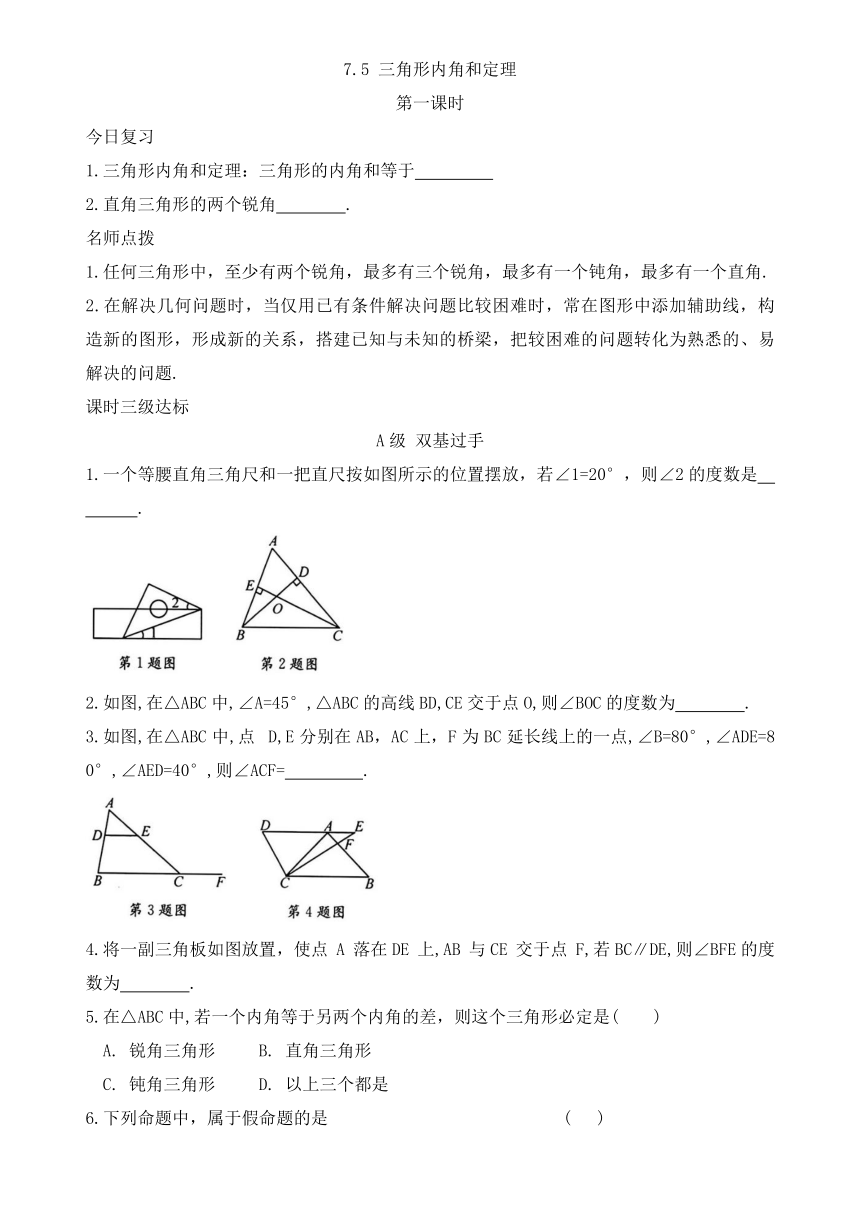
7.5 三角形内角和定理 同步练习（无答案）

7.5 三角形内角和定理 第一课时 今日复习 1.三角形内角和定理：三角形的内角和等于 2.直角三角形的两个锐角 . 名师点拨 1.任何三角形中，至少有两个锐角，最多有三个锐角，最多有一个钝角，最多有一个直角. 2.在解决几何问题时，当仅用已有条件解决问题比较困难时，常在图形中添加辅助线，构造新的图形，形成新的关系，搭建已知与未知的桥梁，把较困难的问题转化为熟悉的、易解决的问题. 课时三级达标 A级 双基过手 1.一个等腰直角三角尺和一把直尺按如图所示的位置摆放，若∠1=20°，则∠2的度数是 . 2.如图,在△ABC中,∠A=45°,△ABC的高线BD,CE交于点O,则∠BOC的度数为 . 3.如图,在△ABC中,点 D,E分别在AB，AC上，F为BC延长线上的一点,∠B=80°,∠ADE=80°,∠AED=40°,则∠ACF= . 4.将一副三角板如图放置，使点 A 落在DE 上,AB 与CE 交于点 F,若BC∥DE,则∠BFE的度数为 . 5.在△ABC中,若一个内角等于另两个内角的差，则这个三角形必定是( ) A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 以上三个都是 6.下列命题中，属于假命题的是 ( ) A. 等角的余角相等 B. 若两个数的绝对值相等，则这两个数也相等 C. 三角形的任意两边之和大于第三边 D. 两直线平行，同位角相等 7.如图,在△ABC中,∠B=50°,∠A=30°,CD平分∠ACB,CE⊥AB于点E，则∠DCE的度数是( ) A.5° B.8° C.10° D.15° 8.如图,在△ABC中,∠A =50°,∠1=30°,∠2=40°,则∠D的度数是( ) A.110° B.120° C.130° D.140° 9.(1)如图, 的顶点F，G 分别落在直线AB，CD上, GE 交 AB 于点 H,GE 平分∠FGD.若. 求∠EFB的度数. (2)如图,在△ABC中,AD是高，AE，BF是角平分线，它们相交于点 O,∠BOA =125°,求∠DAC 的度数. 10.(1)如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为 D,AF 平分∠CAB,交 CD 于点 E,交CB于点F,求证:CE=CF. (2)如图,在 中，BD,CF都是高,M为BC 的中点,N为DF 的中点.求证： B级 能力提升 11.如图,在△ABC中,∠A=40°,将△ABC沿DE折叠,点 A落在点F处,则∠FDB+∠FEC的度数为 . 12. 如图,在△ABC 中,∠BAC=90°,将△ABC 沿EF 折叠,使点 B 落 在 AC 边 上 的点 D 处,若∠ADE= 2 ∠DFC, ∠DFC = 20°, 则∠C= . 13如图, 在 Rt △ABC中,∠ACB = 90°,AC=BC=6,D 为BC 上一点,连接 AD,过点 A 作 AE⊥AD,取 AE=AD,连接 BE 交 AC 于点F.当△AEF 为等腰三角形时,CD= 14.如图,和 都是等腰直角三角形， 的顶点 A在 的斜边 DE上，CD交AB 于点 F,若 求 的面积. C级 综合拓展 15.【背景】在△ABC 中,分别以边 AB,AC 为底,向△ABC 外侧作等腰直角三角形ABD 和等腰直角三角形ACE,∠ADB=∠AEC=90°. 【研究】M 为BC 的中点,连接 DM,EM,研究线段 DM 与EM 的位置关系与数量关系. (1)如图 1,当∠BAC=90°时,延长 EM到点F,使得 MF=ME,连接 BF.此时易证△EMC≌△FMB,D,B,F三点在一条直线上.进一步分析可以得到△DEF 是等腰直角三角形，因此得到线段 DM 与 EM 的位置关系是 ，数量关系是 . (2)如图2,当 时，请继续探究线段 DM 与 EM 的位置关系与数量关系，并证明你的结论. (3)【应用】如图3,当点C,B,D在同一直线上时，连接DE，若 4,求 DE的长. 第二课时 今日复习 1.三角形的外角定义：三角形的一边与另一边的 所组成的角，叫作三角形的外角. 2.三角形的外角定理：三角形的一个外角等于与它 的两个内角的和. 3.三角形的一个外角 任何一个和它不相邻的内角. 名师点拨 1.三角形的外角特征：①顶点是三角形的一个顶点；②外角的一边是三角形的边；③外角的另一条边是三角形某条边的延长线. 2.三角形外角的实质：三角形的外角是一个内角的邻补角，两个角的和等于180°. 3.三角形的两内角平分线所夹钝角等于 90°加上不相邻第三角的一半. 4.三角形的两外角平分线所夹锐角等于 90°减 ... ...