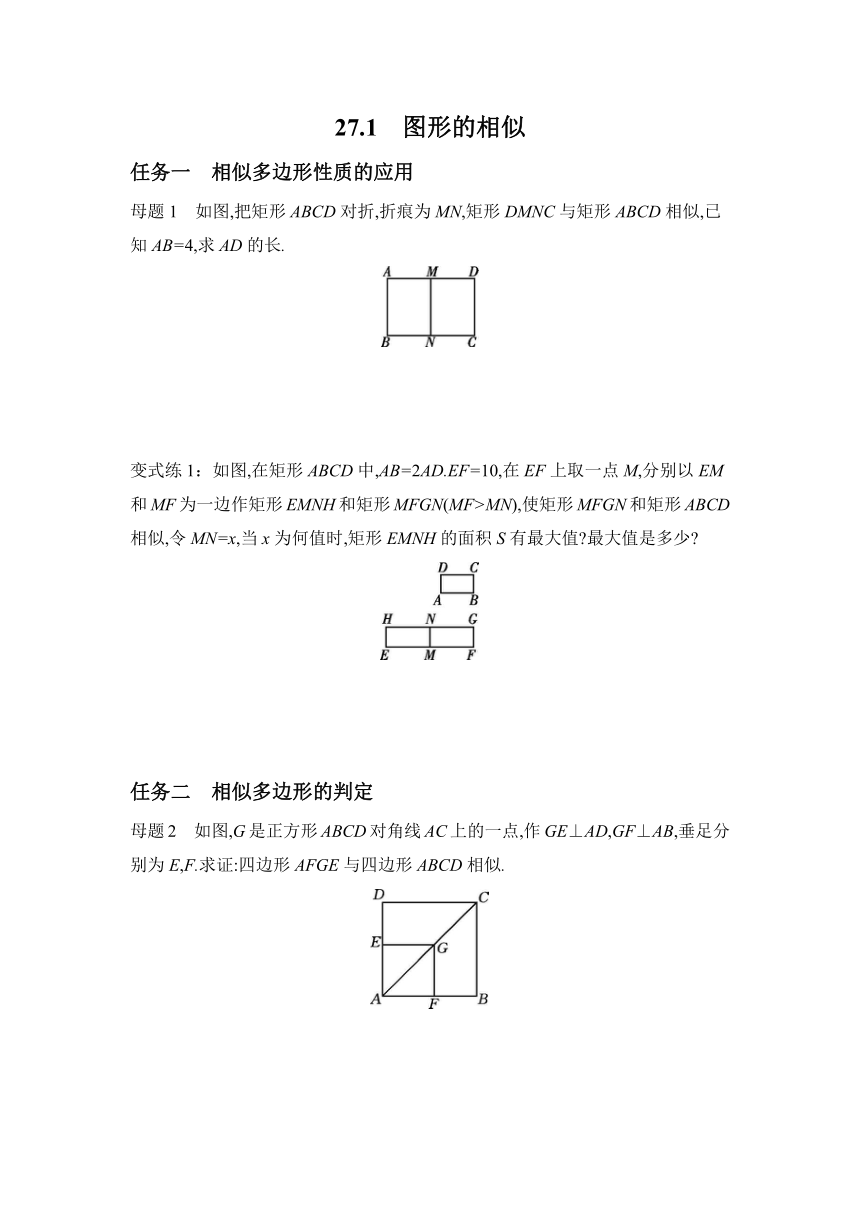
27.1 图形的相似 任务一 相似多边形性质的应用 母题1 如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4,求AD的长. 变式练1:如图,在矩形ABCD中,AB=2AD.EF=10,在EF上取一点M,分别以EM和MF为一边作矩形EMNH和矩形MFGN(MF>MN),使矩形MFGN和矩形ABCD相似,令MN=x,当x为何值时,矩形EMNH的面积S有最大值 最大值是多少 任务二 相似多边形的判定 母题2 如图,G是正方形ABCD对角线AC上的一点,作GE⊥AD,GF⊥AB,垂足分别为E,F.求证:四边形AFGE与四边形ABCD相似. 变式练2:如图,四边形ABCD∽四边形EFGH,连接对角线AC,EG.求证:=. 任务三 相似多边形的性质与判定的综合应用 母题3 在AD=30 m,AB=20 m的矩形花坛四周修筑小路. (1)如图1,如果四周小路的宽均相等,且宽度为x,那么矩形A'B'C'D'和矩形ABCD相似吗 请说明理由. (2)如图2,如果互相平行的两条小路的宽相等,且宽度分别为x,y(y>x),试问:当两条小路的宽x与y的比值为多少时,矩形A'B'C'D'和矩形ABCD相似 请说明理由. 图1 图2 【关键点拨】 变式练3:如图,矩形ABCD纸片的边AB长为2 cm,动直线l分别交AD,BC于E,F两点,且EF∥AB. (1)若直线l是矩形ABCD的对称轴,且沿着直线l剪开后得的矩形EFCD与原矩形CBAD相似,试求AD的长. (2)若使AD=+1 cm,试探究:在AD边上是否存在点E,使剪刀沿着直线l剪开后,所得到的小矩形纸片中存在与原矩形ABCD相似的情况 若存在,请求出AE的值,并判断E点在边AD上位置的特殊性;若不存在,试说明理由. 参考答案 母题1 解:由已知得MN=AB,MD=AD=BC. ∵矩形DMNC与矩形ABCD相似, ∴=. ∵MN=AB,DM=AD,BC=AD, ∴AD2=AB2. 由AB=4,得AD=4. 变式练1 解:∵矩形MFGN和矩形ABCD相似, ∴=. ∵AB=2AD, ∴===2. 又∵MN=x,∴MF=2x. ∵EF=10,∴EM=10-2x. ∴S=x(10-2x)=-2x2+10x=-2x-2+. ∵S是关于x的二次函数,-2<0,x>0, ∴当x=时,S有最大值,最大值为. 母题2 证明:∵GE⊥AD,GF⊥AB,四边形ABCD是正方形, ∴∠GEA=∠EAF=∠GFA=90°,AC平分∠DAB, ∴四边形EAFG为矩形,GE=GF, ∴四边形EAFG为正方形, ∴四边形AFGE与四边形ABCD相似. 变式练2 证明:∵四边形ABCD∽四边形EFGH, ∴=,∠D=∠H, ∴△ADC∽△EHG, ∴=. 母题3 解:(1)不相似.理由如下: 若矩形A'B'C'D'和矩形ABCD相似, 则=, 解得x=0. 因为小路的宽不能为0 m, 所以矩形A'B'C'D'和矩形ABCD不相似. (2)当小路的宽x与y的比值为时,矩形A'B'C'D'和矩形ABCD相似.理由如下: 当矩形A'B'C'D'和矩形ABCD相似时, =,解得=. 所以当小路的宽x与y的比值为时,矩形A'B'C'D'和矩形ABCD相似. 变式练3 解:(1)∵矩形EFCD∽矩形CBAD, ∴=. 又∵CD=AB=2,可设AD=2CF=2x, ∴=, 解得x=, 故AD=2. (2)假设存在矩形EFCD与矩形CBAD相似, 则DC必与AD对应,ED必与DC对应, 有=, ∴DC2=AD·ED. 又∵DC=2 cm,AD=(+1)cm, ∴ED===(-1)cm. ∴AE=AD-(-1)=2(cm). 而AE=2>-1=ED, 依据对称性考虑,必定存在当AE=-1时,使矩形EFBA与矩形ABCD相似的情形. 综上所述,当AE=-1或2时,在剪开所得到的小矩形纸片中必存在与原矩形相似. ... ...
~~ 您好,已阅读到文档的结尾了 ~~