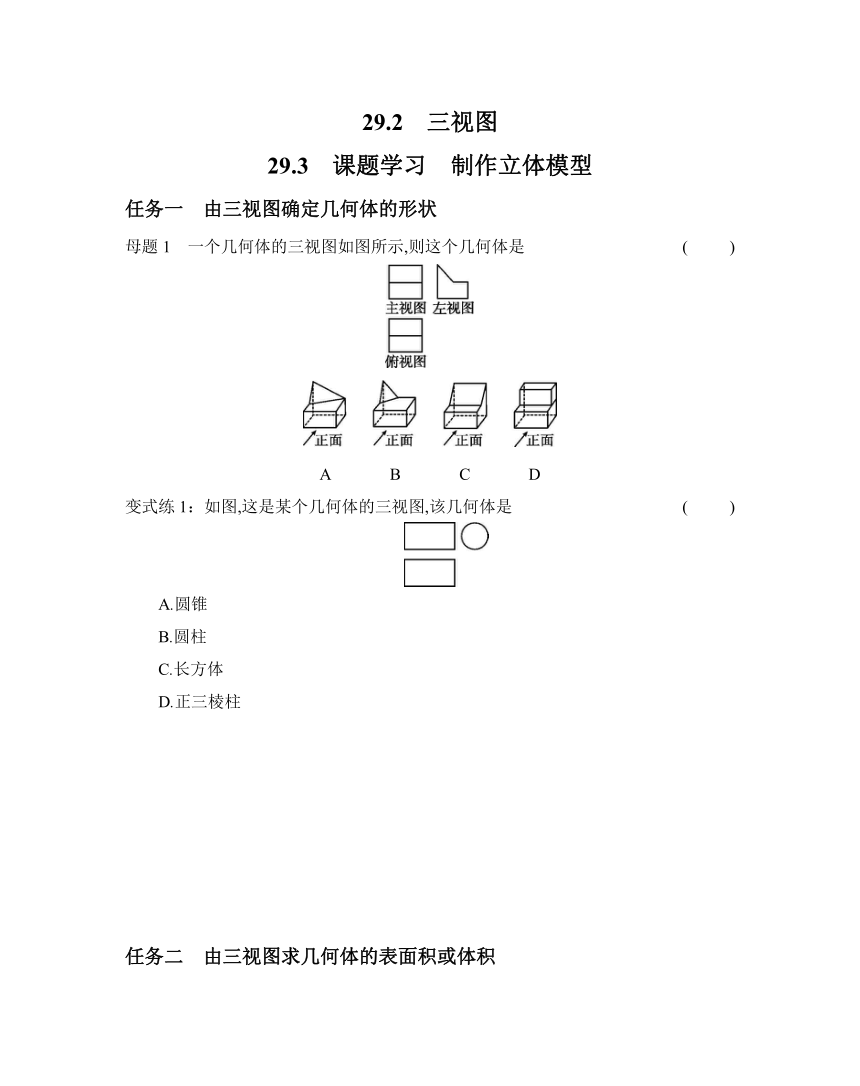
29.2 三视图 29.3 课题学习 制作立体模型 任务一 由三视图确定几何体的形状 母题1 一个几何体的三视图如图所示,则这个几何体是 ( ) A B C D 变式练1:如图,这是某个几何体的三视图,该几何体是 ( ) A.圆锥 B.圆柱 C.长方体 D.正三棱柱 任务二 由三视图求几何体的表面积或体积 子任务1 利用三视图求几何体的表面积 母题2 如图,这是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是 ( ) A.80-2π B.80+4π C.80 D.80+6π 变式练2:某几何体的三视图及相关数据如图所示,则该几何体的侧面积是 ( ) A.8π B.60π C.15π D.4π 子任务2 利用三视图求几何体的体积 母题3 如图,这是一个由铁铸灌成的几何体的三视图,根据图中所标数据,铸灌这个几何体需要的铁的体积为 ( ) A.12π B.18π C.24π D.78π 变式练3:根据如图所示的三视图,求它们表示的几何体的体积(图中标有尺寸). 任务三 由视图推断几何体中 小正方体的个数问题 母题4 如图,这是由一些完全相同的小正方体搭成的几何体的主视图和左视图,则组成这个几何体的小正方体的个数最多为 个,最少为 个. 变式练4:由n个相同的小正方体组成的几何体,其部分视图如图所示,则n的最大值是 ,n的最小值是 . 任务四 巧用三视图求组合体的表面积 母题5 将棱长为a的小正方体摆放成如图所示的形状,请解答下列问题: (1)求该物体的表面积(列出算式,并求出结果). (2)根据图中的摆放方法类推,如果该物体为20层,求该物体的表面积(列出算式,并求出结果). 变式练5:把10个相同的小正方体按如图所示的方式堆放,它的外表面含有若干小正方形.如果将图中标有A的小正方体移走,这时外表面含有的小正方形的个数与移走前相比 ( ) A.不增不减 B.减少1个 B.减少2个 D.减少3个 参考答案 母题1 C 变式练1 B 母题2 B 提示:由三视图可知,该几何体是长方体,中间是空心圆柱体,长方体的长、宽、高分别为4,4,3,圆柱体底面直径为2,高为3, 长方体的表面积为4×4×2+4×3×4=80,圆柱体的侧面积为2π×3=6π,上下表面空心圆的面积为2π, 故这个几何体的表面积是80+6π-2π=80+4π. 故选B. 变式练2 D 提示:观察图形可知, 圆锥的母线长为=2, 所以圆锥的侧面积为πrl=2×2×π=4π. 故选D. 母题3 B 提示:由三视图可得,几何体是空心圆柱,其小圆半径是1,大圆半径是2, 则大圆面积为π×22=4π,小圆面积为π×12=π, 故这个几何体的体积为6×4π-6×π=24π-6π=18π. 故选B. 变式练3 解:根据三视图可以得出此物体是一个长方体和半圆柱的组合体, 其体积V=4×6×2+π×(4÷2)2×2=48+4π. 母题4 10;4 提示:结合主视图和左视图,可知该几何体共两层.由主视图,可知该几何体有三列,且右边两列只有一层;由左视图,可知该几何体有三行,且前两行只有一层.所以小正方体的个数最多的情况:底层小正方体的个数为3×3=9,上面一层有1个小正方体,所以共有小正方体9+1=10(个).小正方体的个数最少的情况:底层小正方体的个数为1+1+1=3,上面一层有1个小正方体,所以共有小正方体3+1=4(个).故答案为10;4. 变式练4 18;12 提示:从俯视图中可以看出最底层小正方体的个数为7, 从主视图可以看出每一层小正方体的层数为3层和中间一层至少3个,最上面至少2个,故n的最小值是7+3+2=12. 综合主视图和俯视图,底面最多有2+3+2=7个,第二层最多有2+3+2=7个,第三层最多有2+0+2=4个,那么n的最大值是7+7+4=18.故答案为18;12. 母题5 解:(1)观察发现,正面、侧面、上面三个方向的视图的面积都为6a2, 故该物体的表面积为6×6a2=36a2. (2)当该物体为20层时,类推可知, 每个方向上均有(1+2+3+…+20)个小正方形, 故其表面积为6×(1+2+3+…+20)×a2=6×21 ... ...
~~ 您好,已阅读到文档的结尾了 ~~