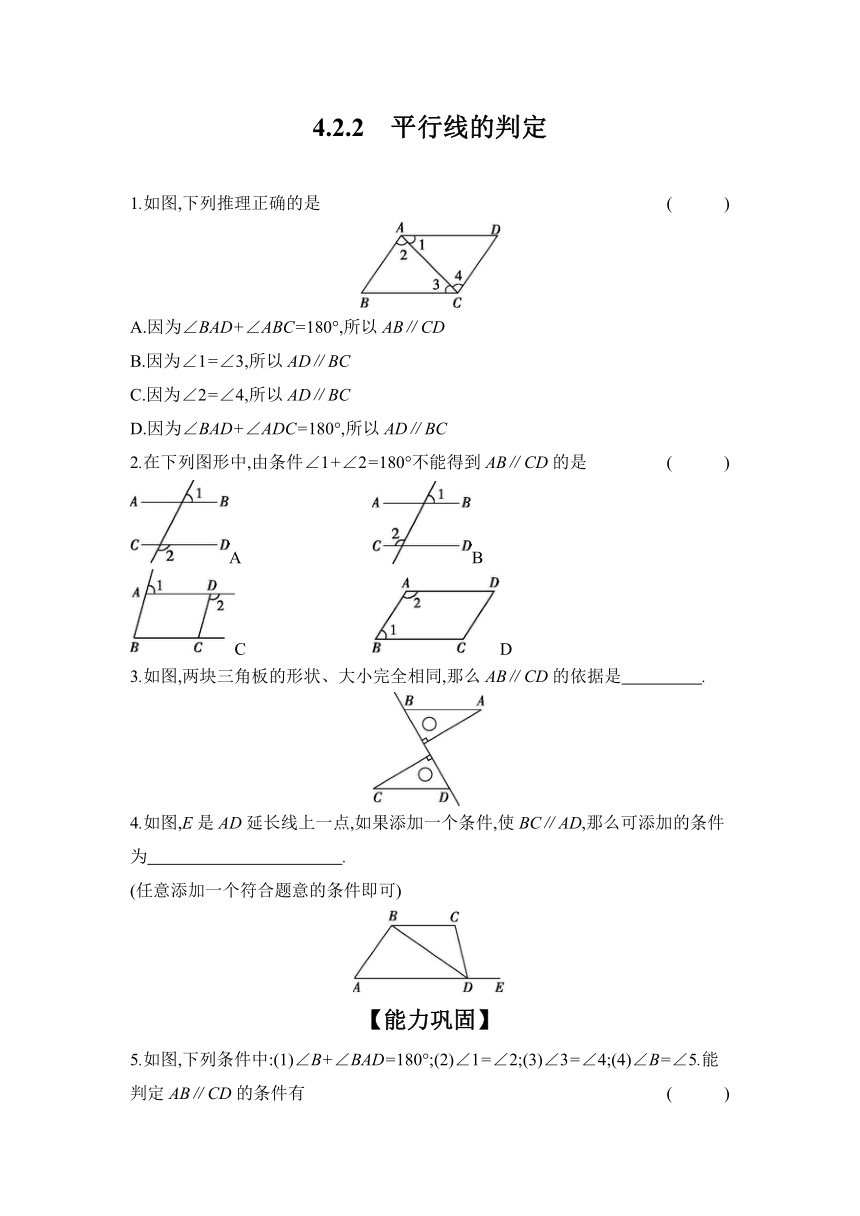
4.2.2 平行线的判定 1.如图,下列推理正确的是 ( ) A.因为∠BAD+∠ABC=180°,所以AB∥CD B.因为∠1=∠3,所以AD∥BC C.因为∠2=∠4,所以AD∥BC D.因为∠BAD+∠ADC=180°,所以AD∥BC 2.在下列图形中,由条件∠1+∠2=180°不能得到AB∥CD的是 ( ) A B C D 3.如图,两块三角板的形状、大小完全相同,那么AB∥CD的依据是 . 4.如图,E是AD延长线上一点,如果添加一个条件,使BC∥AD,那么可添加的条件为 . (任意添加一个符合题意的条件即可) 【能力巩固】 5.如图,下列条件中:(1)∠B+∠BAD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.能判定AB∥CD的条件有 ( ) A.1个 B.2个 C.3个 D.4个 6.将一块直角三角板ABC按如图所示的方式放置,其中∠ABC=30°,A,B两点分别落在直线m,n上,∠1=20°,添加下列哪个条件可使直线m∥n ( ) A.∠2=20° B.∠2=30° C.∠2=45° D.∠2=50° 7.如图,∠A=70°,O是AB上一点,∠AOD=100°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 . 8.将两块直角三角板的直角顶点C按如图所示的方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°. (1)①若∠DCB=45°,则∠ACB的度数为 ; ②若∠ACB=140°,则∠DCE的度数为 . (2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由. (3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由). 【素养拓展】 9.在同一方格中,下列选项中的直线,与图中的线段平行的是 ( ) A B C D 10.如图,直线AB和CD被直线EF所截. (1)如图1,EG平分∠BEF,FH平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足什么数量关系时,AB∥CD 并说明理由. (2)如图2,EG平分∠MEB,FH平分∠DFE(平分的是一对同位角),则∠1与∠2满足什么数量关系时,AB∥CD 并说明理由. (3)如图3,EG平分∠AEF,FH平分∠DFE(平分的是一对内错角),则∠1与∠2满足什么条件时,AB∥CD 为什么 参考答案 1.B 2.D 3.内错角相等,两直线平行 4.∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE 【能力巩固】 5.B 6.D 7.10° 8.解:(1)①∵∠DCB=45°,∠ACD=90°, ∴∠ACB=∠ACD+∠DCB=90°+45°=135°. ②∵∠ACB=140°,∠ECB=90°,∴∠ACE=140°-90°=50°,∴∠DCE=90°-∠ACE=90°-50°=40°. (2)猜想:∠ACB+∠DCE=180°.理由如下: ∵∠ACE=90°-∠DCE,∠ACB=∠ACE+90°, ∴∠ACB=90°-∠DCE+90°=180°-∠DCE, 即∠ACB+∠DCE=180°. (3)30°或45°.当CB∥AD时,∠ACE=30°;当EB∥AC时,∠ACE=45°. 【素养拓展】 9.C 10.解:(1)当∠1+∠2=90°时,AB∥CD.理由如下: ∵EG平分∠BEF,FH平分∠DFE,∴∠BEF=2∠1,∠DFE=2∠2.∵∠1+∠2=90°,∴∠BEF+∠DFE=180°,∴AB∥CD. (2)当∠1=∠2时,AB∥CD.理由如下: ∵EG平分∠BEM,FH平分∠DFE,∴∠BEM=2∠1,∠DFE=2∠2.∵∠1=∠2,∴∠BEM=∠DFE,∴AB∥CD. (3)当∠1=∠2时,AB∥CD.理由如下: ∵EG平分∠AEF,FH平分∠DFE,∴∠AEF=2∠1,∠DFE=2∠2.∵∠1=∠2,∴∠AEF=∠DFE,∴AB∥CD. ... ...
~~ 您好,已阅读到文档的结尾了 ~~