人教版八年级数学上名师点拨精练第13章 轴对称专题证明线段相等的思路归纳（含解析）

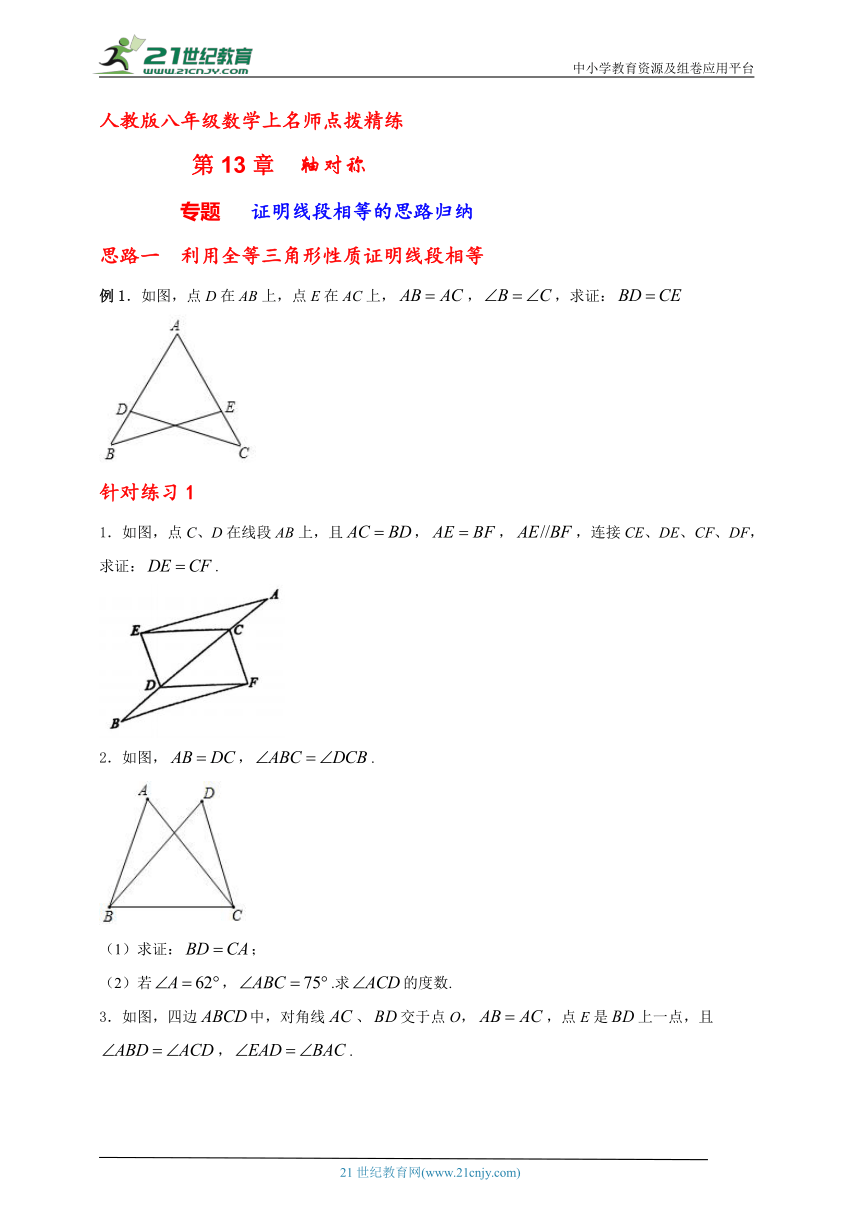
中小学教育资源及组卷应用平台 人教版八年级数学上名师点拨精练 轴对称 专题 证明线段相等的思路归纳 思路一 利用全等三角形性质证明线段相等 例1．如图，点D在AB上，点E在AC上，，，求证： 针对练习1 1．如图，点C、D在线段AB上，且，，，连接CE、DE、CF、DF，求证：. 2．如图，，. （1）求证：； （2）若，.求的度数. 3．如图，四边中，对角线、交于点O，，点E是上一点，且，. （1）求证：； （2）若，，求的长. 4．如图所示，，，.求证：. 5 .如图，点E在上，，且，连接并延长，交的延长线于点F． (1)求证：； (2)若，，求的度数． 思路二 利用等腰三角形的性质与判定证明线段相等 例2-1 .如图，点，在的边上，，． (1)如图1，求证：； (2)如图2，当时，过点作于点，如果，求的值． 针对练习2 1．如图，在四边形中，，，平分交于点E．求证：． 2．如图，为中线，点E在上，交于点F，，求证：． 3．已知：如图，， 求证：． 4．如图，中，，点D在的延长线上，连接平分交于点E，过点E作，垂足为点F，与相交于点G．． (1)求证：； (2)若，，求和的度数； (3)求证：． 5 .如图，在中，，，D为BC的中点，过D作直线DE交直线AB与E，过D作直线，并交直线AC与F． (1)若E点在线段AB上（非端点），则线段DE与DF的数量关系是_____； (2)若E点在线段AB的延长线上，请你作图（用黑色水笔），此时线段DE与DF的数量关系是_____，请说明理由． 思路三 利用线段垂直平分线的性质和判定证明线段相等 例3-1 .如图8，在△ABC中，AB＝AC，∠BAC＝120°，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F. 求证：BM＝MN＝CN. 图8 针对练习3 1．如图，在中，，，AC的垂直平分线DE分别交AB，AC于点D，E. （1）求证：是等腰三角形； （2）若的周长是13，，求AC的长. 2．如图,△ABC中,∠ABC=45 ,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G. （1）求证:BF=AC; （2）求证:CE= BF 3．已知：如图，在△ABC中，120°＜∠BAC＜180°，AD为边BC的垂直平分线，以AC为边作等边三角形ACE，△ACE与△ABC在直线AC的异侧，直线BE交DA的延长线于点F，连接FC交AE于点M． （1）求证：∠FEA＝∠FBA． （2）求∠EFC的度数． （3）猜想线段FE，FA，FD之间的数量关系，并证明你的结论． 4．如图，在中，的垂直平分线分别交于点D，E．求证：． 思路四 利用角平分线的性质与判定证明线段相等 例4 .如图，△ABC中，AD是∠BAC的平分线，E、F分别为AB、AC上的点，连接DE、DF，∠EDF＋∠BAC＝180°．求证：DE＝DF． 针对练习4 1．如图，在中，AD是它的角平分线，且，，，垂足分别为E，F.求证. 2．如图,中,AD是的平分线,,,E,F为垂足,连接EF交AD于G. （1）求证:. （2）试判断AD与EF的位置关系,并说明理由. 3．如图所示，的外角的平分线CF与的平分线BG相交于点O.求证：点O到三边AB，BC，AC的距离相等. 4．如图，D为BC的中点，于点D，交的平分线AE于点E, 于点F, 交AC的延长线于点G.求证：. 5．如图1，在中，，，AD,CE分别是，的平分线，AD,CE相交于点F. （1）判断FE与FD之间的数量关系，并说明理由； （2）如图2，如果不是直角，其他条件不变，（1）中所得结论是否仍然成立？请说明理由. 人教版八年级数学上名师点拨精练 轴对称 专题 证明线段相等的思路归纳 思路一 利用全等三角形性质证明线段相等 例1．如图，点D在AB上，点E在AC上，，，求证： 答案：证明见解析 解析：证明：在和中， ∵， ， ， . 针对练习1 1．如图，点C、D在线段AB上，且，，，连接CE、DE、CF、DF，求证：. 答案：见解析 解析：， ， 即：， ， ， ， ， . 2．如图，，. （1）求证：； （2）若，.求的度数. 答案：（1）见详解 （2） 解析：（ ... ...