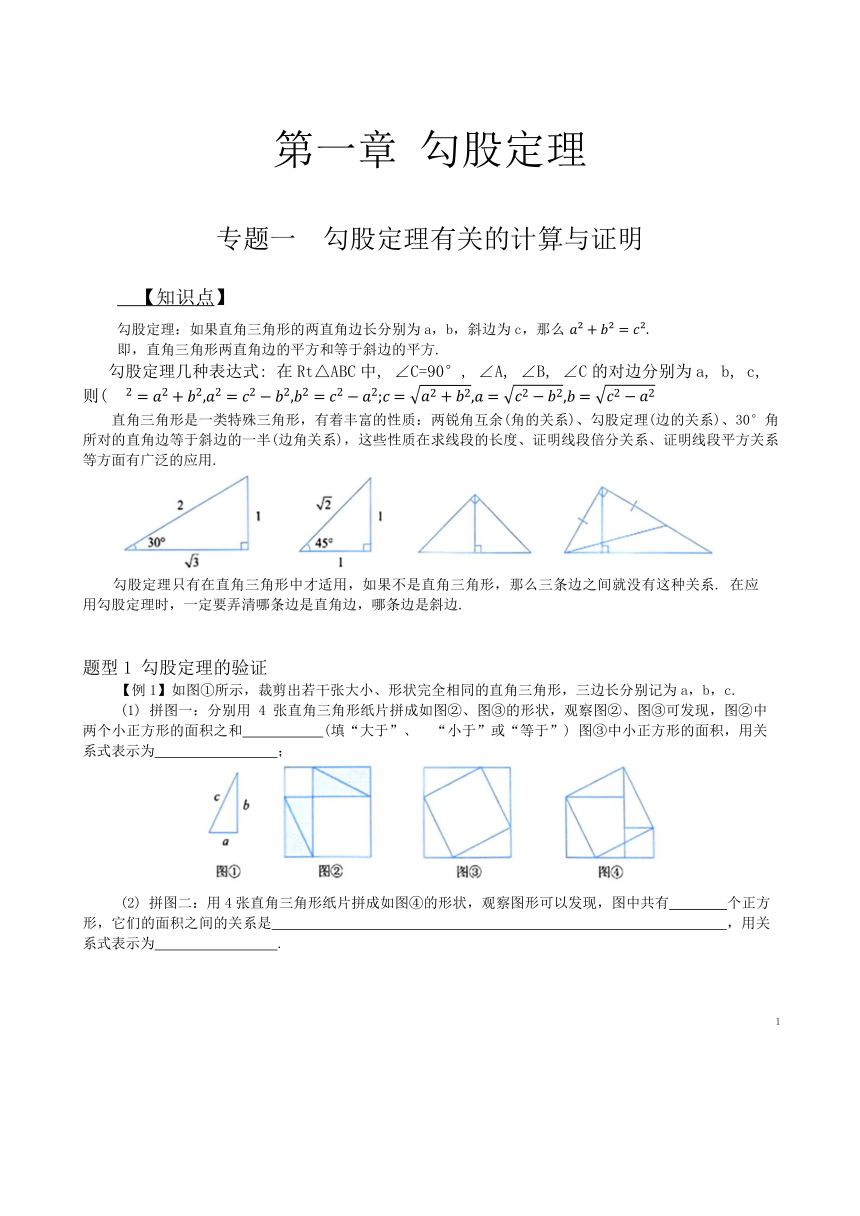
第一章 勾股定理 专题一 勾股定理有关的计算与证明 【知识点】 勾股定理:如果直角三角形的两直角边长分别为a,b,斜边为c,那么 即,直角三角形两直角边的平方和等于斜边的平方. 勾股定理几种表达式: 在Rt△ABC中, ∠C=90°, ∠A, ∠B, ∠C的对边分别为a, b, c, 则( 直角三角形是一类特殊三角形,有着丰富的性质:两锐角互余(角的关系)、勾股定理(边的关系)、30°角所对的直角边等于斜边的一半(边角关系),这些性质在求线段的长度、证明线段倍分关系、证明线段平方关系等方面有广泛的应用. 勾股定理只有在直角三角形中才适用,如果不是直角三角形,那么三条边之间就没有这种关系. 在应用勾股定理时,一定要弄清哪条边是直角边,哪条边是斜边. 题型1 勾股定理的验证 【例1】如图①所示,裁剪出若干张大小、形状完全相同的直角三角形,三边长分别记为a,b,c. (1) 拼图一:分别用 4 张直角三角形纸片拼成如图②、图③的形状,观察图②、图③可发现,图②中两个小正方形的面积之和 (填“大于”、 “小于”或“等于”) 图③中小正方形的面积,用关系式表示为 ; (2) 拼图二:用4张直角三角形纸片拼成如图④的形状,观察图形可以发现,图中共有 个正方形,它们的面积之间的关系是 ,用关系式表示为 . 1 ·举一反三 1. 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图①或图②摆放时,都可以用“面积法”来证明, 下面是小聪利用图①证明勾股定理的过程: 将两个全等的直角三角形按图①所示摆放,其中∠DAB=90°,求证: 证明: 连结DB, 过点D作BC边上的高DF, 则DF=EC=b-a. 因为 又因为 所以 所以 请参照上述证法,利用图②完成下面的证明. 将两个全等的直角三角形按图②所示摆放,其中∠DAB=90°. 求证: 题型2 “弦图”的应用 【例2】如图所示,在边长为10的正方形ABCD 中,内接有六个大小相同的正方形,点 P,Q,M,N 是落在大正方形边上的小正方形的顶点,求每个小正方形的面积. 。举一反三。 2. 长方形ABCD中嵌入了如图所示的5个相同的正方形和一个三角形,E,F,G,H分别在长方形的边 AB, BC, CD和DA 上. 已知. 求嵌入的图形总面积. 题型3 利用勾股定理求直角三角形中线段的长 【例3】如图所示,在. 中, D 是斜边AB的中点, E, F分别在边AC, BC上, 若 ,求线段AB的长度. 举一反三。 3. 如图所示,在 中, 点D是AC的中点, 点E在边 BC上, 求AE的长. 3 题型4 应用勾股定理求一般三角形中线段的长 【例4】如图所示,在. 中, ,以AC 为边向外作等边 求BD的长. ·举一反三· 4. 如图所示, 在四边形ABCD中, 求 BD的长. 题型5 线段多解求解型问题 【例5】在 中, ,以AB为边向外作等腰直角三角形ABD,求CD的长. 4 举一反三。 5.在 中, .以AC为一边,在 的外部作等腰直角三角形ACD,求线段BD的长. 题型6 利用勾股定理求解动点运动问题 【例6】如图所示,等腰三角形ABC的底边 BC为8cm, 腰长为5cm, 一动点 P在底边 BC上从 B向C以0.25cm/s的速度运动. 请你探究:当点P运动多长时间时,点P与顶点A的连线PA 与腰垂直 举一反三。 6. 一个正方体物体沿斜坡向下滑动,其截面如图所示,正方形 DEFH的边长为2m,坡角 当正方形DEFH运动到什么位置,即当AE的长为多少时,有 5 题型7 特殊角与勾股定理 【例7】如图, 在△ACD中, 中, AB=AC. (1) 如图①, 若 ,在△ACD外作等边△ADD'. 求证: 求BD的长. (2) 如图②, 若∠ , 求BD的长. 举一反三。 7.(1)如图①, 中分别以AB,AC为边向外作等腰 和等腰 连接BD, CE, 若 求BD的长. (2) 如图②, 四边形ABCD中, 连接AC, ( 5,求AD的长. 6 题型8 利用勾股定理探索规律 【例8】如图①所示,在 的边 AB 的同侧,分别以三边为直径作 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

