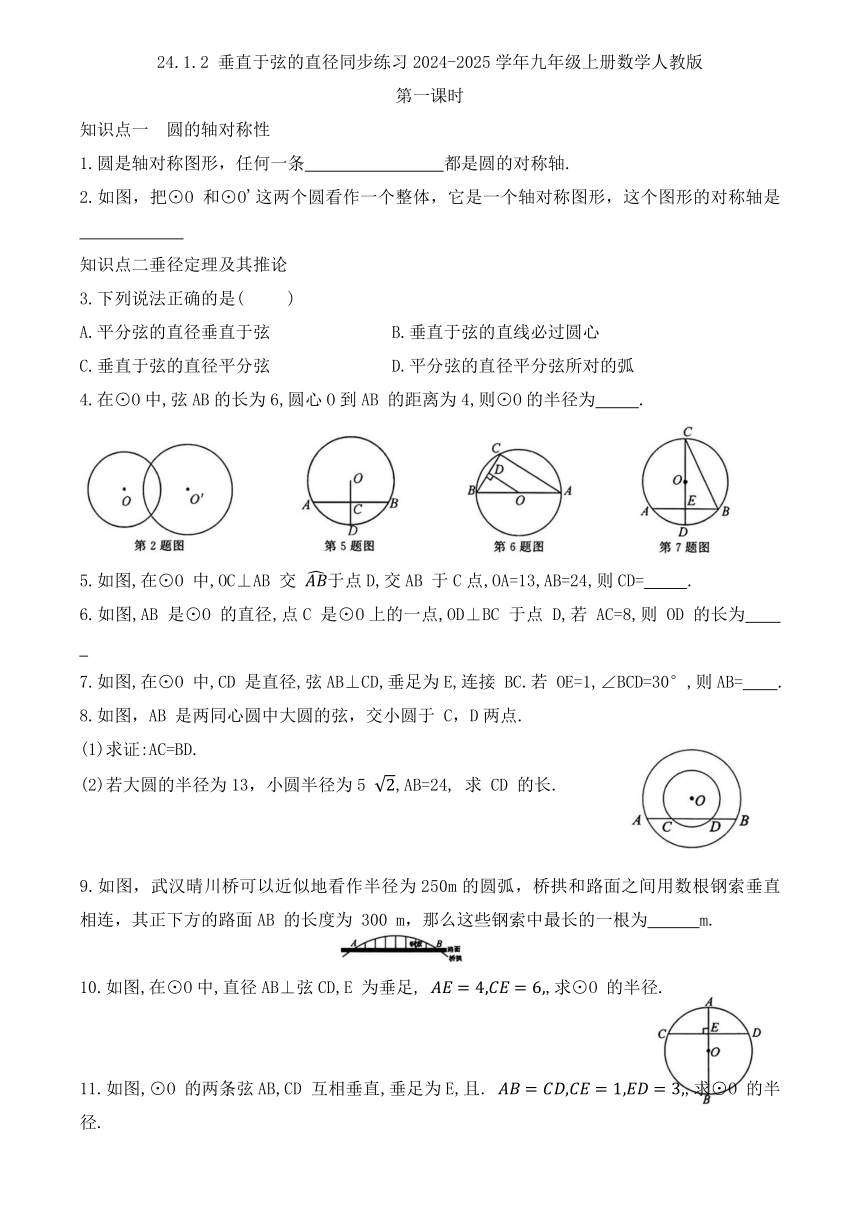
24.1.2 垂直于弦的直径同步练习（2课时，无答案）2024-2025学年九年级上册数学人教版

24.1.2 垂直于弦的直径同步练习2024-2025学年九年级上册数学人教版 第一课时 知识点一 圆的轴对称性 1.圆是轴对称图形，任何一条 都是圆的对称轴. 2.如图，把⊙O 和⊙O'这两个圆看作一个整体，它是一个轴对称图形，这个图形的对称轴是 知识点二垂径定理及其推论 3.下列说法正确的是( ) A.平分弦的直径垂直于弦 B.垂直于弦的直线必过圆心 C.垂直于弦的直径平分弦 D.平分弦的直径平分弦所对的弧 4.在⊙O中,弦AB的长为6,圆心O到AB 的距离为4,则⊙O的半径为 . 5.如图,在⊙O 中,OC⊥AB 交 于点D,交AB 于C点,OA=13,AB=24,则CD= . 6.如图,AB 是⊙O 的直径,点C 是⊙O上的一点,OD⊥BC 于点 D,若 AC=8,则 OD 的长为 7.如图,在⊙O 中,CD 是直径,弦AB⊥CD,垂足为E,连接 BC.若 OE=1,∠BCD=30°,则AB= . 8.如图，AB 是两同心圆中大圆的弦，交小圆于 C，D两点. (1)求证:AC=BD. (2)若大圆的半径为13，小圆半径为5 ,AB=24, 求 CD 的长. 9.如图，武汉晴川桥可以近似地看作半径为250m的圆弧，桥拱和路面之间用数根钢索垂直相连，其正下方的路面AB 的长度为 300 m，那么这些钢索中最长的一根为 m. 10.如图,在⊙O中,直径AB⊥弦CD,E 为垂足, ,求⊙O 的半径. 11.如图,⊙O 的两条弦AB,CD 互相垂直,垂足为E,且. ,求⊙O 的半径. 12.如图,某地有一座圆弧形拱桥,桥下水面宽度AB 为 7.2m ,拱高CD为 2.4 m. (1)求拱桥的半径； (2)现有一艘宽3m、船舱顶部为长方形并高出水面2m 的货船要经过这里，此货船能顺利通过拱桥吗 13.已知△ABC 内接于⊙O,AB=AC,O 到BC的距离为6,⊙O 的半径为10. (1)如图1,当圆心O在△ABC 外部时,求 AB 的长; (2)如图2,当圆心O在△ABC 内部时,求 AB 的长. 14.在半径为5的⊙O 中,弦AB=6,弦CD=8,且 则 AB 与CD 之间的距离为 . 第二课时 知识点一 利用垂径定理证明与计算 1.如图,已知⊙O的半径为13,弦AB 长为24,则点O到AB 的距离是 . 2.如图,在⊙O中,半径OD 垂直于弦AB,垂足为C,CD=2,AB=8,则OC= . 3.如图,已知AB 为⊙O 的直径,且AB=15cm,弦CD⊥AB 于M,若OM:OA=3:5,则CD长为 cm. 知识点二 过圆心作弦的垂线用勾股———单勾股 4.在直径为200cm的圆柱形油槽内装入一些油以后，截面如图.若油面的宽AB=160cm,则油的最大深度为 cm. 5.如图,PG 平分∠EPF,点O在射线OG上,⊙O交PE、PF 于C、D、A、B 四点,OA∥PE,⊙O的半径为5,AB=8,则OP= . 6.如图，圆弧形桥拱的跨度AB=12米，拱高CD=4米，则拱桥的半径为 米. 7.“老碗”(如图)的形状示意图. 是⊙O 的一部分，D 是 的中点，连接OD，与弦AB 交于点C,连接OA,OB.已知AB=24 cm,碗深CD=8cm,求⊙O 的半径OA 的长. 8.如图,BD 是⊙O的弦,点C 在BD上,以 BC 为边作等边△ABC,点 A 在圆内,且AC 恰好经过点O,其中 BC=12,OA=8,则⊙O的半径为( ) A.10 C.2 9.如图,AB 为⊙O 的直径,AB=8,DE 为弦,DC⊥AB 于C,M 为DE 的中点,则CM 长的最大值为( ) A. CD 的长 B. DE 的长 C.4 D.5 10.如图,在 Rt△ABC 中,∠C=90°,AC=4,BC=3,以C 为圆心,CB 为半径的圆交AB 于点P,则PB 的长为 . 11.在⊙O 中,半径r=1,弦. ,则∠BAC的度数为( ) A.75° B.15° C.15°或 75° D.60° 12.如图,AB 为⊙O 的弦,半径OC⊥AB 于E 点, ,求 AB 的长. 13.如图,AB 为⊙O 的直径,正方形 CDEF 的 CD 边在 AB 上,E、F 在⊙O 上,正方形 CMNG 的顶点 N 在⊙O上,点 M 在 AB 上,点 G 在 CF 上,若 EF=4,求 MN 的长. 14.在由小正方形组成的网格中，A、B、C均在格点上，⊙O经过点A、B、C. (1)在图1中,作 (2)在图 2 中,作 (3)在图3中,作 (4)在图 4 中,⊙O 与格线交于D,作 ... ...