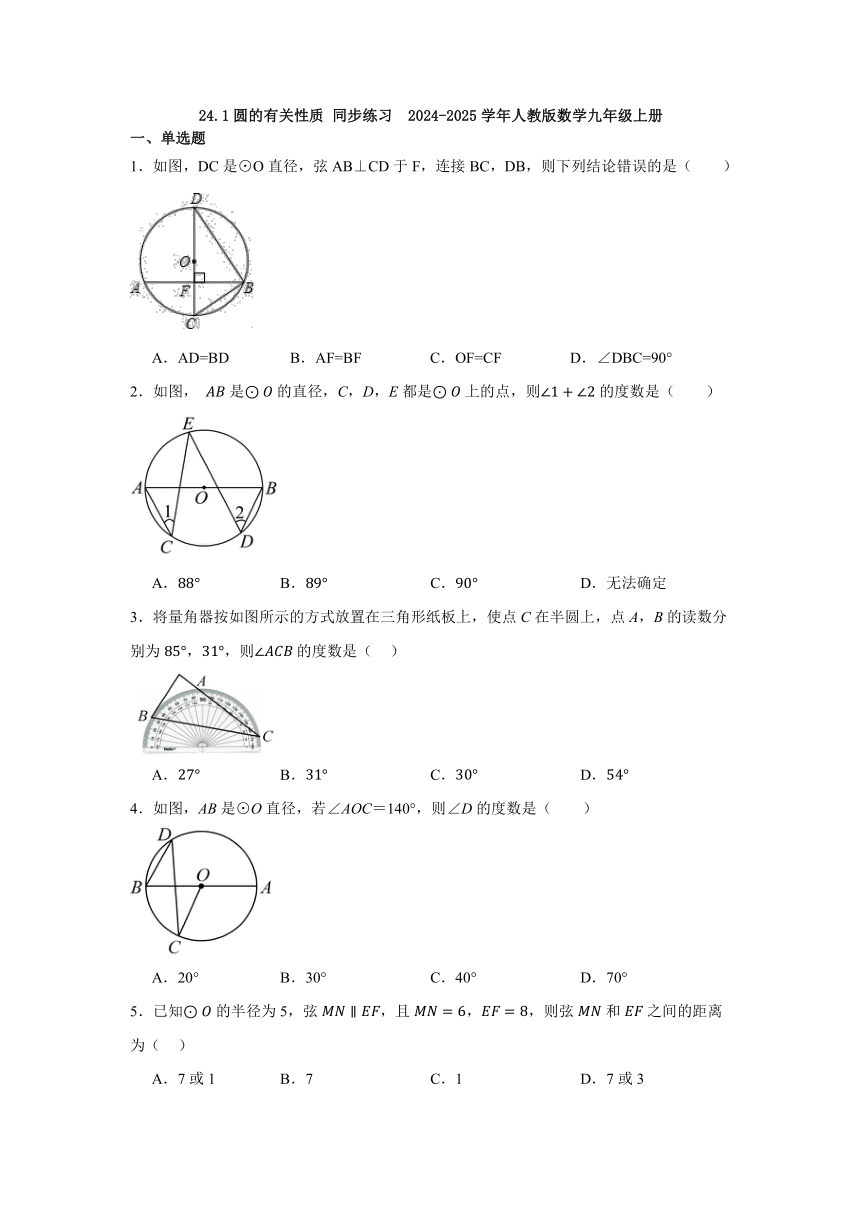
24.1圆的有关性质 同步练习 （含答案）2024-2025学年人教版数学九年级上册

24.1圆的有关性质 同步练习 2024-2025学年人教版数学九年级上册 一、单选题 1．如图，DC是⊙O直径，弦AB⊥CD于F，连接BC，DB，则下列结论错误的是（　　） A．AD=BD B．AF=BF C．OF=CF D．∠DBC=90° 2．如图， 是的直径，C，D，E都是上的点，则的度数是（　　） A． B． C． D．无法确定 3．将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上，点A，B的读数分别为，，则的度数是（ ） A． B． C． D． 4．如图，AB是⊙O直径，若∠AOC＝140°，则∠D的度数是（　　） A．20° B．30° C．40° D．70° 5．已知的半径为5，弦，且，，则弦和之间的距离为（ ） A．7或1 B．7 C．1 D．7或3 6．如图，点A、B在上，点C在弧上，若，则（ ） A． B． C． D． 7．如图，已知：是的直径，、是上的三等分点，，则是（ ） A． B． C． D． 8．若圆的一条弦把圆分成度数之比为1：3的两条弧，则这条弦所对的圆周角等于（　　） A．45° B．135° C．90°或270 D．45°或135° 9．如图，中，，P是平面上的一个点，连接，，已知始终为直角，则线段长的最大值为（　　） A．6 B． C． D．5 二、填空题 10．如图，点A，B，C是⊙O上的点，AO＝AB，则∠ACB＝ 度． 11．如图，是的弦，半径于点，连接并延长，交于点连接．若，则的面积为 ． 12．如图，四边形为的内接四边形，已知，则的度数为 ． 13．如图，点P（1，2），⊙P经过原点O，交y轴正半轴于点A，点B在⊙P上，∠BAO＝45°，则点B的坐标是 ． 14．如图，为的直径，点C，点D在上，并且在直径的两侧，，则 ． 15．将半径为5的如图折叠，折痕长为6，C为折叠后的中点，则长为 ． 16．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=16厘米，则球的半径为 厘米． 17．如图，在⊙O内有折线DABC，点B，C在⊙O上，DA过圆心O，其中OA＝8，AB＝12，∠A＝∠B＝60°，则BC＝ ． 三、解答题 18．如图，在中，AB是的直径，与AC交于点D，，求的度数． 19．已知：如图，A，B，C，D是⊙O上的点，且AB=CD，求证：∠AOC=∠BOD． 20．如图，一条公路的转弯处是一段圆弧 用直尺和圆规作出所在圆的圆心O；要求保留作图痕迹，不写作法 若的中点C到弦AB的距离为，求所在圆的半径． 21．如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.已知AB＝2DE,∠AEC＝25°,求∠AOC的度数. 22．如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分．如果M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E，CD=10，EM=25．求⊙O的半径． 23．如图，中，，以为直径作，交于点，交于点． (1)求证：； (2)若，求的度数． 24．如图，AB是⊙O的直径，CD是弦，AB与CD相交于点E，连接AC、AD，AC＝AD． （1）求证：AB⊥CD． （2）若AB＝12，BE＝2，求CD的长． 参考答案： 1．C 2．C 3．A 4．A 5．A 6．C 7．C 8．D 9．C 10．150． 11． 12． 13．(3,1)或( 1,3)． 14． 15．3 16．10 17．20 18．解：在中，， 是⊙的直径，⊙与AC交于点D， ∴． 19．解：∵AB＝CD ∴弧AB＝弧CD ∴弧AC＝弧BD ∴∠AOC＝∠BOD． 20．解：如图1， 点O为所求； 连接交AB于D，如图2， 为的中点， ， ， 设的半径为r，则， 在中，， ，解得， 即所在圆的半径是50m． 21．解：连接OD，如图 ∵AB=2DE=2OD ∴OD=DE 又∵∠E=25° ∴∠DOE=∠E=25° ∴∠ODC=50° 同理∠C=∠ODC=50° ∴∠AOC=∠E+∠OCE=75° 22．如图，连接OC， ∵M是弦CD的中点，EM过圆心O， ∴EM⊥CD． ∴CM=MD． ∵CD=10， ∴CM=5． 设OC=x，则OM=25-x， 在Rt△COM中，根据勾股定理，得 52+（25-x）2=x2． 解得 x=13． ∴⊙O的半径为13． 23．（1）证明：连接，如图1所示： 是的直径， ， ， ， ， ． （2）解：连接，如图2所示： 是的直径， 是半径， ， ... ...