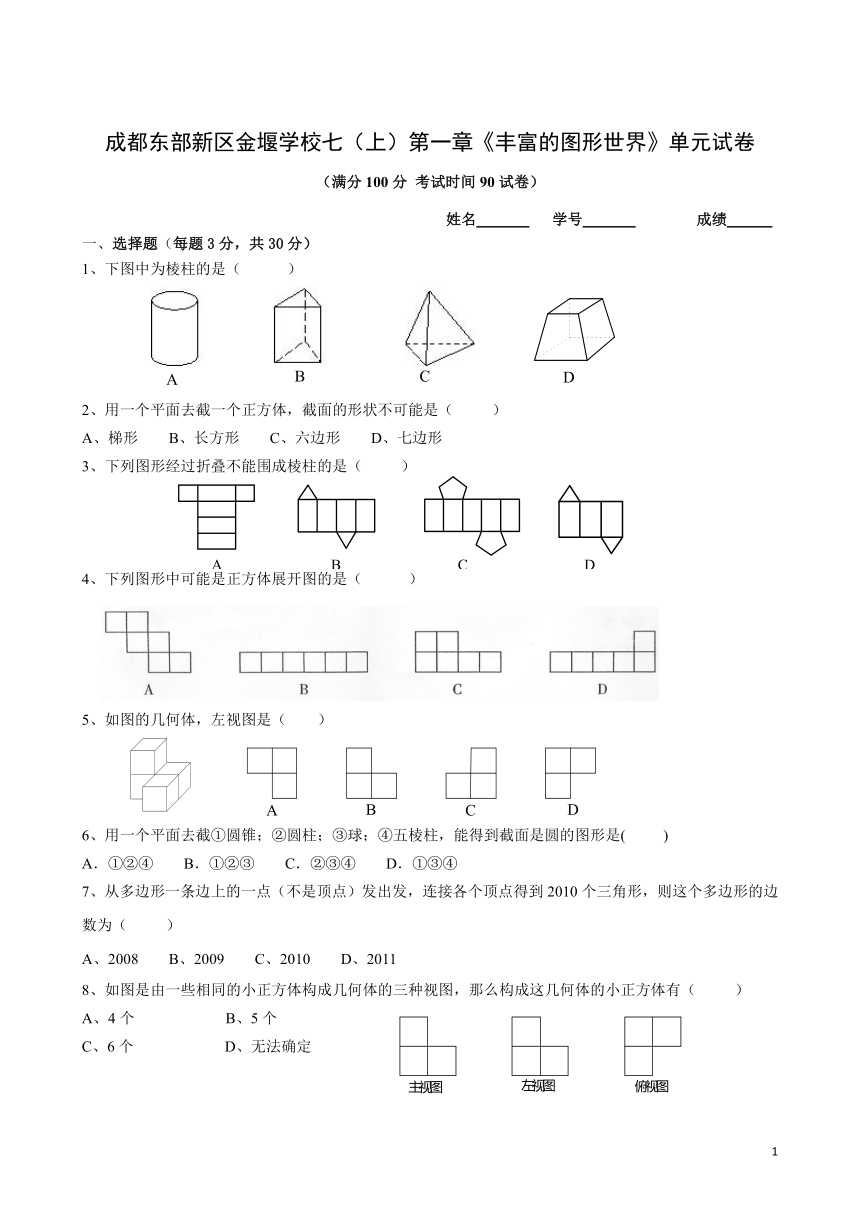
成都东部新区金堰学校七(上)第一章《丰富的图形世界》单元试卷 (满分100分 考试时间90试卷) 姓名 学号 成绩 一、选择题(每题3分,共30分) 1、下图中为棱柱的是( ) 2、用一个平面去截一个正方体,截面的形状不可能是( ) A、梯形 B、长方形 C、六边形 D、七边形 3、下列图形经过折叠不能围成棱柱的是( ) 4、下列图形中可能是正方体展开图的是( ) 5、如图的几何体,左视图是( ) 6、用一个平面去截①圆锥;②圆柱;③球;④五棱柱,能得到截面是圆的图形是( ) A.①②④ B.①②③ C.②③④ D.①③④ 7、从多边形一条边上的一点(不是顶点)发出发,连接各个顶点得到2010个三角形,则这个多边形的边数为( ) A、2008 B、2009 C、2010 D、2011 8、如图是由一些相同的小正方体构成几何体的三种视图,那么构成这几何体的小正方体有( ) A、4个 B、5个 C、6个 D、无法确定 9、如图是正方体的表面展开图,折叠成正方体后,其中哪两个完全相同?( ) A、(1)(2) B、(2)(3) C、(3)(4) D、(2)(4) 10、明明用纸(如下图左)折成了一个正方体的盒子,里面装了一瓶墨水,混放在下面的盒子里,只凭观察,选出墨水在哪个盒子中?( ) 二、填空题:(每小题3分,共21分) 1、将下列几何体分类,柱体有: ,锥体有 ,球体有 2、圆柱的底面是 ,侧面是 ,展开后的侧面是 ;圆锥的底面是 ,侧面是 ,展开后的侧面是 3、用一个平面去截一个正方体,截面可能是 4、若要使下图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为6,则x=_ ___,y=_____。 5、三棱柱有 个面 个顶点 条棱,四棱柱有 个面 个顶点 条棱,五棱柱有 个面 个顶点 条棱,……,由此可以推测n棱柱有_____个面,____个顶点,_____条棱。 6、用小立方块搭一几何体,使得它的主视图和俯视图如下图所示,这样的几何体最少要_____个立方块,最多要____个立方块。 7.如图,是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是 .(把下图中正确的立体图形的序号都填在横线上) 三、画图题: (每小题6分,共18分) 1、把第一行的图形绕虚线转一周,能形成第二行的某个几何体,用线连起来。 2、下图是由七块积木搭成,这几块积木都是相同的正方体,请画出这个图形的主视图、左视图和俯视图。 3、如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数。请你画出它的主视图与左视图。 四、解答题(每小题6分,3题7分,共31分) 1、已知一个长方体的长为4cm,宽为3cm,高为5cm,请求出: (1)长方体所有棱长的和;(2)长方体的表面积; 2、如图,已知一个由小正方体组成的几何体的左视图和俯视图。 (1)该几何体最少需要几块小正方体?(2)最多可以有几块小正方体? 3、(1)用一个平面截三棱柱,截面形状可能有 (2)用一个平面截长方体,截面形状可能有 (3)用一个平面截五棱柱,截面形状可能有 (注:本题中长方形、正方形、梯形、平行四边形都以四边形计) 由此,用平面去截棱柱,你发现了什么规律?(答两条) 4、如图所示的几何体是由若干个相同的小正方体组合而成的(第一层1个;第二层3个;第3层6个),小正方体的一个侧面的面积为1cm。今要用红颜色给这个几何体的表面着色(包含底面),要着色的面积是多少 5、把棱长为1cm的若干个小正方体摆放如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)。 (1)该几何体中有多少小正方体?(2)画出主视图;(3)求出涂上颜色部分的总面积。 8 ... ...
~~ 您好,已阅读到文档的结尾了 ~~