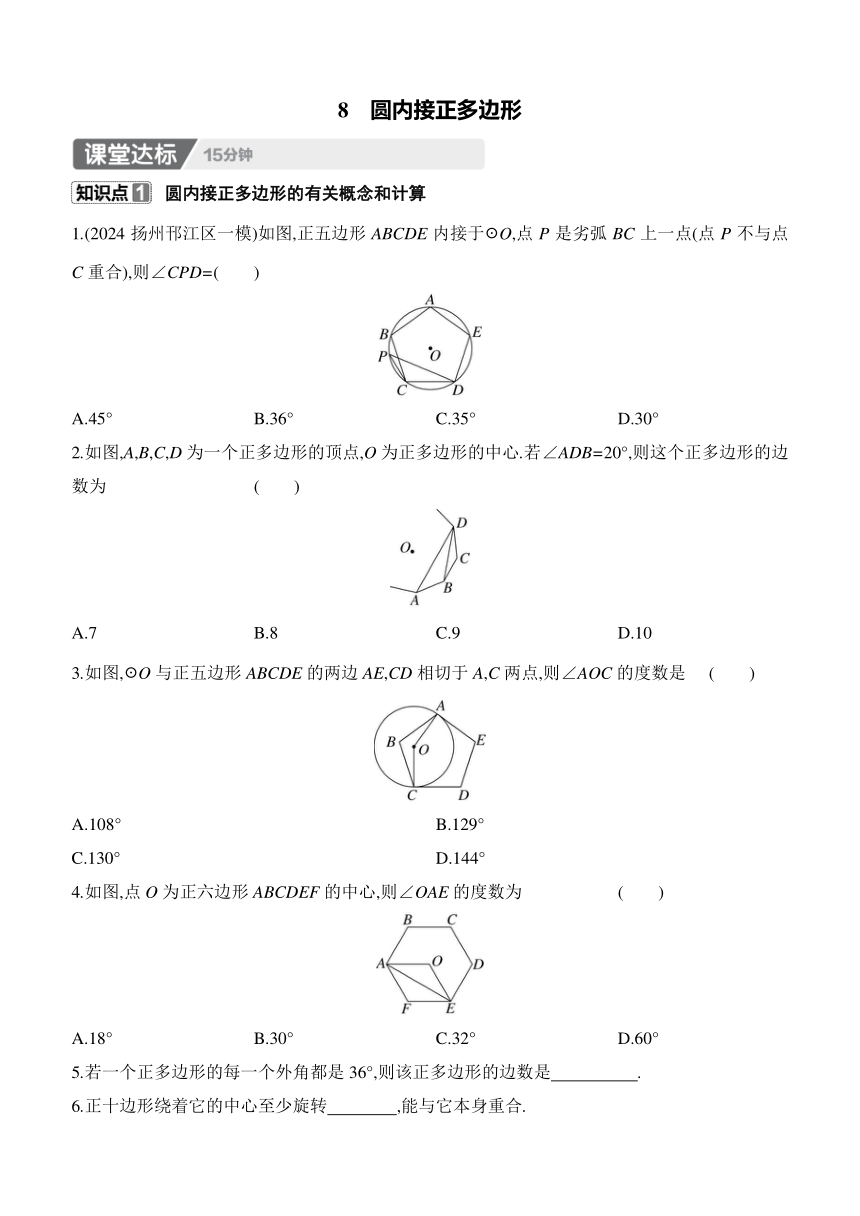
8 圆内接正多边形 圆内接正多边形的有关概念和计算 1.(2024扬州邗江区一模)如图,正五边形ABCDE内接于☉O,点P是劣弧BC上一点(点P不与点C重合),则∠CPD=( ) A.45° B.36° C.35° D.30° 2.如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心.若∠ADB=20°,则这个正多边形的边数为 ( ) A.7 B.8 C.9 D.10 3.如图,☉O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是 ( ) A.108° B.129° C.130° D.144° 4.如图,点O为正六边形ABCDEF的中心,则∠OAE的度数为 ( ) A.18° B.30° C.32° D.60° 5.若一个正多边形的每一个外角都是36°,则该正多边形的边数是 . 6.正十边形绕着它的中心至少旋转 ,能与它本身重合. 7.如图,在正六边形ABCDEF中,连接AC,若AC=6,则正六边形的边长为 . 8.(2024宿迁期末)如图,正六边形ABCDEF内接于☉O,☉O的半径为4. (1)求正六边形的边心距; (2)求正六边形ABCDEF的面积. 圆内接正多边形的作图 9.如图,用尺规作圆内接正六边形、内接正三角形、内接正方形.(不写作法,保留作图痕迹) 内接正六边形 内接正三角形 内接正方形 1.如图,☉O是正六边形ABCDEF的外接圆.若☉O的半径为6,则四边形ACDF的周长是 ( ) A.6+6 B.12+6 C.12+12 D.6+12 2.如图,M是正六边形EFGHPQ的中心.在平面直角坐标系中,若点M的坐标为(0,0),点E的坐标为(-1,0),则点H的坐标为 ( ) A.(-2,0) B.(1,1) C.(1,0) D.(2,0) 3.如图,正五边形ABCDE中,M,N分别是CD,DE的中点,连接AM,BN相交于点O,那么∠AOB的度数为 . 4.(2024咸阳永寿县模拟)如图,点O是正八边形ABCDEFGH的中心,连接BD,若BD=6,则点O到BD的距离为 . 5.如图,六边形ABCDEF是☉O的内接正六边形,设四边形ABCE的面积为S1,△ACE的面积为S2,则= . 6.如图,正六边形ABCDEF内接于☉O. (1)若P是上的动点,连接BP,FP,求∠BPF的度数; (2)已知△ADF的面积为2,求☉O的面积. 7.(几何直观)如图,☉O为△ABC的外接圆,半径长为5,∠BAC=∠BOC=120°. (1)求BC的长. (2)作∠BAC的平分线交☉O于点D. ①求证:△BDC为等边三角形; ②若AC=6,求AD的长. 【详解答案】 课堂达标 1.B 解析:如图,连接OC,OD, ∵五边形ABCDE是正五边形, ∴∠COD==72°, ∴∠CPD=∠COD=36°. 故选B. 2.C 解析:如图,连接OA,OB, ∵A,B,C,D为一个正多边形的顶点,O为正多边形的中心, ∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上, ∵∠ADB=20°, ∴∠AOB=2∠ADB=40°, ∴这个正多边形的边数==9. 故选C. 3.D 解析:∵五边形ABCDE是正五边形, ∴∠D=∠E==108°. 又∵☉O与正五边形ABCDE的两边AE,CD相切于A,C两点, ∴∠OAE=∠OCD=90°. 在五边形CDEAO中, ∠AOC=(5-2)×180°-90°×2-108°×2=144°, 故选D. 4.B 解析:如图,连接OF, ∵点O为正六边形ABCDEF的中心, ∴∠AOF=∠EOF=60°, ∴∠AOE=120°. 在等腰三角形AOE中, ∠OAE=×(180°-120°)=30°. 故选B. 5.10 解析:∵一个正多边形的每一个外角都是36°, ∴边数=360°÷36°=10. 6.36° 解析:∵360°÷10=36°, ∴该图形绕中心至少旋转36°后能与它本身重合. 7.2 解析:如图,连接BE,交AC于点H, ∵六边形ABCDEF是正六边形, ∴AB=BC,BE⊥AC,∠ABC=120°, ∴AH=CH=AC=3,∠AHB=90°,∠BAH=30°, ∴AB==2, ∴正六边形的边长为2. 8.解:(1)如图,连接OC,OD,过点O作OH⊥CD于点H,则∠OHC=∠OHD=90°. ∵六边形ABCDEF是正六边形, ∴∠COD=60°,∴△COD为等边三角形. ∴∠COH=30°, ∴=cos∠COH=cos 30°,∵OC=4, ∴圆心O到CD的距离OH=4×cos 30°=2, 即正六边形的边心距为2. (2)由(1)得CD=OC=4,正六边形ABCDEF的面积=6S△COD=×4×2×6=24. 9.解:如图. 内接正六边形 内接正三角形 内接正方形 课后提升 1.C 解析:如图,连接OA ... ...
~~ 您好,已阅读到文档的结尾了 ~~

